Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi \(M\left(0;y\right)\) thì ta có :
\(\overrightarrow{AB}=\left(-3;4\right)\) ; \(\overrightarrow{AM}=\left(-1;y-2\right)\)
Để A,B,M thẳng hàng thì \(\overrightarrow{AB}=k.\overrightarrow{AM}\) , tức là :
\(\begin{cases}k.\left(-1\right)=-3\\k.\left(y-2\right)=4\end{cases}\) \(\Rightarrow\begin{cases}k=3\\y=\frac{10}{3}\end{cases}\)
Vậy để A,B,M thẳng hàng thì \(M\left(0;\frac{10}{3}\right)\)
Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.
Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
Bài 38:
Thay phương trình d2 vào d1 ta được:
\(2\left(-1+3t\right)+\left(2+t\right)-7=0\)
\(\Leftrightarrow7t-7=0\Rightarrow t=1\)
\(\Rightarrow\left\{{}\begin{matrix}m=-1+3t=2\\n=2+t=3\end{matrix}\right.\)
\(\Rightarrow P=7\)
Bài 39:
Gọi tọa độ A(a;0) và tọa độ B(0;b)
Do M là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}\frac{a+0}{2}=3\\\frac{b+0}{2}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=6\\b=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(6;0\right)\\B\left(0;2\right)\end{matrix}\right.\)
Phương trình AB: \(\frac{x}{6}+\frac{y}{2}=1\Leftrightarrow x+3y-6=0\)
Bài 40:
d có 1 vtcp là \(\left(3;-4\right)\)
Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' có 1 vtpt là \(\left(3;-4\right)\)
Phương trình d':
\(3\left(x-2\right)-4\left(y+5\right)=0\Leftrightarrow3x-4y-26=0\)
N là giao của d và d' nên tọa độ N thỏa mãn:
\(3\left(-7+3t\right)-4\left(2-4t\right)-26=0\Rightarrow t=\frac{11}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x_N=-7+3t=-\frac{2}{5}\\y_N=2-4t=-\frac{34}{5}\end{matrix}\right.\) \(\Rightarrow N\left(-\frac{2}{5};-\frac{34}{5}\right)\)
Bài 35:
Do \(AB//CD\) nên đường thẳng AB nhận \(\left(2;5\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x-4\right)+5\left(y+1\right)=0\Leftrightarrow2x+5y-3=0\)
Bài 36:
Do đường thẳng song song trục hoành nên có dạng \(y=a\)
Do đường thẳng qua A(1;3) nên pt là \(y=3\)
Bài 37:
Do thẳng thẳng vuông góc trục hoành nên có dạng \(x=a\)
Đường thẳng qua A(1;3) nên có pt: \(x=1\)
Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến
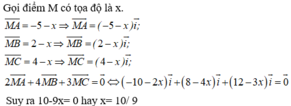
Chọn B.
Ta có M nằm trên trục Oy nên tọa độ điểm M có dạng M(0; y)
Ba điểm A; B; M thẳng hàng khi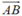
cùng phương với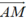 
Ta có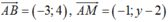
. Do đó, 
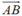cùng phương với
Vậy M(0; 10) .