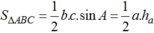Cho tam giác ABC có b = 7; c = 5, cosA = 3/5. Đường cao ha của tam giác ABC là A. B. 6. C. ...
Đọc tiếp
Cho tam giác ABC có b = 7; c = 5, cosA = 3/5. Đường cao ha của tam giác ABC là
A. 
B. 6.
C. 
D. 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 7 2017
Ta có: cosC = a 2 + b 2 − c 2 2 a b = 6 2 + 7 2 − 10 2 2.6.7 < 0
⇒ C ^ > 90 0
Suy ra, tam giác ABC là tam giác tù.
Chọn B
CM
16 tháng 4 2017
Nửa chu vi của tam giác ABC là: p = 5 + 6 + 7 2 = 9
Áp dụng công thức Hê- rông, diện tích tam giác ABC là:
S = 9. 9 − 5 . 9 − 6 . 9 − 7 = 36.6 = 6 6 .
Chọn C.
10 tháng 3 2022
\(\widehat{A}=180^o-30^o-44^o=106^o.\)
Áp dụng định lý sin ta có:
\(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}=\dfrac{AB}{sinC}.\)
\(\Rightarrow\dfrac{BC}{sin106^o}=\dfrac{7}{sin44^o}=\dfrac{AB}{sin30^o}.\)
\(\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{7.sin106^o}{sin44^o}\approx9,7.\\AB=\dfrac{7.sin30^o}{sin44^o}\approx5,0.\end{matrix}\right.\) (đvđd).
\(S_{\Delta ABC}=\dfrac{1}{2}AB.AC.\sin A\approx\dfrac{1}{2}.5,0.7.\sin106^o\approx17,4\) (đvdt).
\(S=pr=\dfrac{AB+AC+BC}{2}.r.\\ \Rightarrow17,4\approx\dfrac{5,0+7+9,7}{2}.r.\)
\(\Rightarrow r\approx1,6\) (đvđd).
CM
30 tháng 3 2017
a. Do BC > AC > AB ⇒ ∠A > ∠B > ∠C
Ta có AB2 + AC2 = 62 + 82 = 100 = 102 = BC2
Vậy tam giác ABC vuông tại A (1 điểm)
NN
1
Z
21 tháng 11 2021
\(A^o,B^o,C^o\)lần lượt tỉ lệ với 7:7:16
\(\Rightarrow\frac{A^o}{7}=\frac{B^o}{7}=\frac{C^o}{16}\)và \(A^o+B^o+C^o=180^o\)( Tổng 3 góc trong của tam giác )
Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\frac{A^o}{7}=\frac{B^o}{7}=\frac{C^o}{16}=\frac{A^o+B^o+C^o}{7+7+16}=\frac{180^o}{30}=6^o\)
=> góc A = 42o , góc B = 42o , góc C = 96o
Chọn A.
Áp dụng định lí cosin trong tam giác ta có:
a2 = b2 + c2 = 2bc.cosA = 72 + 52 - 2.7.5.3/5 = 32
Nên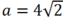
Mặt khác: sin2A + cos2A = 1 nên sin2A = 1 - cos2A = 16/25
Mà sinA > 0 nên sinA = 4/5
Mà: