Cho tam giác ABC vuông tại A có AB=6 cm ; AC= 8cm
a) Tính độ dài đoạn BC .
b) Vẽ AH vuông góc BC tại H . Trên HC lấy D sao cho HD= HB . Chứng minh AB =AD .
c) Trên tia đối của tia HA lấy điểm E sao cho EH= AH . Chứng minh ED vuông góc AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2022
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
3 tháng 2 2022
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có \(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3.6\left(cm\right)\)
3: Xét ΔBAC có BK là đường phân giác
nên \(\dfrac{AK}{KC}=\dfrac{AB}{BC}\)
mà \(\dfrac{AB}{BC}=\dfrac{BH}{AB}\)
nên \(\dfrac{AK}{KC}=\dfrac{BH}{AB}\left(1\right)\)
Xét ΔAHC vuông tại H và ΔBHA vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\)
Do đó: ΔAHC\(\sim\)ΔBHA
Suy ra: \(\dfrac{AC}{AB}=\dfrac{AH}{BH}\)
=>BH/AH=AB/AC
hay \(\dfrac{BH}{AB}=\dfrac{AH}{AC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AK}{KC}=\dfrac{AH}{AC}\)
hay \(AK\cdot AC=AH\cdot KC\)
HS
3
D
18 tháng 4 2017
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, có:
\(AC^2+AB^2=BC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(=10^2-6^2=100-36=64\)
\(\Rightarrow AC=\sqrt{64}=8\)
Ta có: BC>AC>AB
Áp dụng định lí quan hệ giữa góc và cạnh đối diện, ta có:
\(\widehat{A}>\widehat{B}>\widehat{C}\)
KV
5 tháng 5 2023
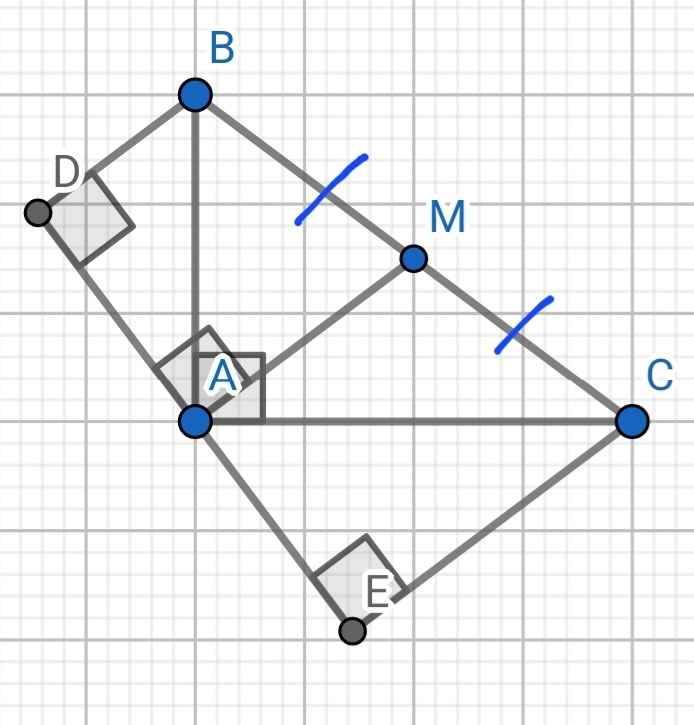
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC
Giải:
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
= 10 : 2 = 5 (cm)
∆AMC có AM = CM = 5 (cm)
⇒ ∆AMC cân tại M
⇒ ∠MAC = ∠MCA (hai góc ở đáy)
Do MA ⊥ DE (gt)
CE ⊥ DE (gt)
⇒ MA // DE
⇒ ∠MAC = ∠ACE (so le trong)
Mà ∠MAC = ∠MCA (cmt)
⇒ ∠MAC = ∠ACE
⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)
Xét hai tam giác vuông:
∆ABC và ∆EAC có:
∠BCA = ∠ACE (cmt)
⇒ ∆ABC ∽ ∆EAC (g-g)
b) Do ∆ABC ∽ ∆EAC (cmt)
⇒ AC/CE = BC/AC
⇒ CE = AC²/BC
= 8²/10
= 6,4 (cm)
4 tháng 9 2017
Vì SABC=37,5=>AH.BC=75=>BC=12,5
Đặt cạnh CH=x
=>HB=12,5-x
Áp dụng hệ thức 2 vào tam giác abc
AH2=BH.CH
<=>62=x(12,5-x)
<=>36=12,5x-x2
<=>x2-12,5x+36=0
<=>(x-6,25)2=3
..............tìm x sau đó thay vào tìm ab,ac
HD
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 12 2021
Áp dụng định lý Pitago:
\(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=24\left(cm^2\right)\)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
b.Xét tam giác vuông ABH và tam giác vuông ADH, có:
HD = HB ( gt )
AH: cạnh chung
Vậy tam giác vuông ABH = tam giác vuông ADH ( 2 cạnh góc vuông )
=> AB = AD ( 2 cạnh tương ứng )