Phần tự luận (6 điểm) SVIP

Hướng dẫn giải:

a) $5^2$ . $36$ + $64$ . $5^2$

=  $5^2$ . $(36 + 64)$

=  $25$ . $100$

=  $2$ $500$.

b) $255 - 5$ . $[82 - (3^2$ . $4 + 9)]$

=  $255 - 5$ . $[82 - 9$ . $(4 + 1)]$

=  $255 - 5$ . $[82 - 45]$

=  $255 - 5$ . $37$

=  $255 - 185$

=  $70$.

Hướng dẫn giải:

a) Viết tập hợp các số tự nhiên không vượt quá 6.

{0; 1; 2; 3; 4; 5; 6}.

b) Tìm tập hợp BC(45 , 30)?

$45 = 3^2$ . $5$ và $30 = 2$ . $3$ . $5$.

BCNN($45$ , $30$) = $2$ . $3^2$ . $5 = 90$.

Vậy BC($45$ , $30$) = $\{0; \, 90; \, 180; \, ...\}$.

c) Một đội y tế tỉnh gồm 144 bác sĩ và 36 y tá lên đường vào miền Nam tham gia tuyến đầu chống dịch. Cần chia đội y tế thành các tổ để ở các tổ có cùng số y tá và có cùng số bác sĩ thì có thể chia thành nhiều nhất bao nhiêu tổ?

Số tổ cần tìm là ƯCLN(144 , 36)

Do 144 $\vdots$ 36 nên ƯCLN(144 , 36) = 36.

Để ở các tổ có cùng số y tá và có cùng số bác sĩ thì có thể chia thành nhiều nhất 36 tổ.

Hướng dẫn giải:

a) Ô đất hình vuông trồng hoa có cạnh bằng $2$m.

Diện tích ô đất trồng hoa đó là:

$S_1 = 2^2 = 4$ (m$^2$).

b) Gọi độ dài cạnh mảnh vườn ban đầu là $x$ (m).

Phần vườn mở rộng gồm 4 hình vuông cạnh $2$m và 4 hình chữ nhật có các kích thước $2$m và $x$ m.

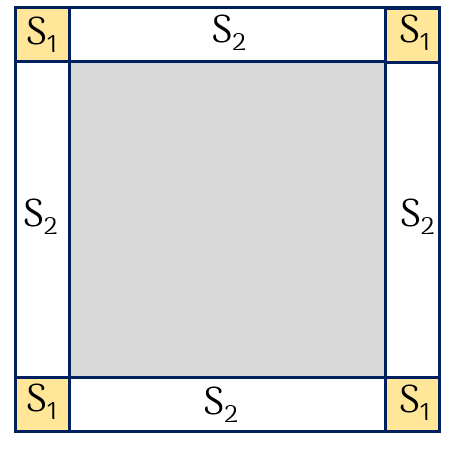
Diện tích 4 hình vuông cạnh $2$m là:

$4S_1 = 4.4 = 16$ (m$^2$).

Diện tích 4 hình chữ nhật có các kích thước $2$m và $x$ m là:

$4S_2 = 4.(2.x) = 8x$ (m$^2$).

Tổng diện tích tăng thêm là $88$ m$^2$ nên:

$4S_1 + 4S_2 = 16 + 8x = 88$

$8x = 72$

$x = 9$ (m).

Chu vi mảnh vườn ban đầu là:

$C = 4 . 9 = 36$ (m).

Hướng dẫn giải:

Theo giả thiết:

$\overline{cd} + 3.2^2.\overline{ab} = (\overline{cd} + 12.\overline{ab})$ $\vdots$ $11$

Ta có:

$\overline{abcd} = \overline{ab}$ . $100 + \overline{cd}$

$= \overline{ab}$ . $88 + \overline{ab}$ . $12 + \overline{cd}$

$= \overline{ab}$ . $8$ . $11 + (\overline{ab}$ . $12 + \overline{cd})$

Vì $(\overline{ab}$ . $8$ . $11)$ $\vdots$ $11$ và $(\overline{ab}$ . $12 + \overline{cd})$ $\vdots$ $11$.

Nên $\overline{abcd}$ $\vdots$ $11$.