Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Lũy thừa với số mũ tự nhiên SVIP
1. Lũy thừa
Lũy thừa bậc \(n\) của \(a\), kí hiệu là \(a^n\), là tích của \(n\) thừa số \(a\):
Ta đọc \(a^n\) là "\(a\) mũ \(n\)" hoặc "\(a\) lũy thừa \(n\)" hoặc "lũy thừa bậc \(n\) của \(a\)";
Số \(a\) được gọi là cơ số, \(n\) được gọi là số mũ.
Phép nhân nhiều thừa số bằng nhau được gọi là phép nâng lên lũy thừa.
\(a^2\) còn được gọi là "\(a\) bình phương" hay "bình phương của \(a\)";
\(a^3\) còn được gọi là "\(a\) lập phương" hay "lập phương của \(a\)".
Quy ước: \(a^1=a\).
Ví dụ 1:
\(2.2.2.2=2^4\).
\(2^4\) đọc là "hai mũ bốn" hoặc "hai lũy thừa bốn" hoặc "lũy thừa bậc bốn của hai"; cơ số là 2 và số mũ là 4.
Ví dụ 2: Tính lũy thừa sau: \(10^4\).
Giải
\(10^4=10.10.10.10=1\) \(000\).
Ví dụ 3: Viết 16 dưới dạng lũy thừa của 2.
Giải
\(16=2.2.2.2=2^4\).
2. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
\(a^m.a^n=a^{m+n}\).
Ví dụ 4: Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:
a) \(3^2.3^6\);
b) \(5.5^6\).
Giải
a) \(3^2.3^6=3^{2+6}=3^8\).
b) \(5.5^6=5^1.5^6=5^{1+6}=5^7\).
3. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ:
\(a^m:a^n=a^{m-n}\) \(\left(a\ne0;m\ge n\right)\).
Quy ước: \(a^0=1\).
Ví dụ 5: Viết kết quả mỗi phép tính sau dưới dạng lũy thừa:
a) \(4^6:4^2\);
b) \(5^3:125\).
Giải
a) \(4^6:4^2=4^{6-2}=4^4\).
b) \(5^3:125=5^3:5^3=5^{3-3}=5^0\).

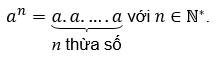
Bạn có thể đánh giá bài học này ở đây