Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

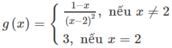
có tập xác định là D = R
- Nếu x ≠ 2 thì 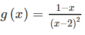
là hàm phân thức hữu tỉ, nên nó liên tục trên các khoảng (-∞; 2) và (2; +∞)
Tại x = 2: 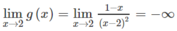
Vậy hàm số y = g(x) không liên tục tại x = 2
Kết luận: y = g(x) liên tục trên các khoảng (-∞; 2) và (2; +∞) nhưng gián đoạn tại x = 2

`TXĐ: R`
`@` Nếu `x > 2` thì: `f(x)=2x+1`
H/s xác định trên `(2;+oo)`
`=>` H/s liên tục trên `(2;+oo)`
`@` Nếu `x < 2` thì: `f(x)=x^2-3x+4`
H/s xác định trên `(-oo;2)`
`=>` H/s liên tục trên `(-oo;2)`
`@` Nếu `x=2` thì: `f(x)=5`
`lim_{x->2^[-]} (x^2-3x+4)=2`
`lim_{x->2^[+]} (2x+1)=5`
Vì `lim_{x->2^[-]} f(x) ne lim_{x->2^[+]} f(x) =>\cancel{exists} lim_{x->2} f(x)`
`=>` H/s gián đoạn tại `x=2`
KL: H/s liên tục trên `(-oo;2)` và `(2;+oo)`
H/s gián đoạn tại `x=2`

1.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{x+2}+\sqrt{2-x}}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Vậy cần bổ sung \(f\left(0\right)=\dfrac{\sqrt{2}}{2}\) để hàm liên tục tại \(x=0\)
2.
a. \(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+\dfrac{3}{2}\right)=\dfrac{3}{2}\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}{x\left(\sqrt[]{x+1}+1\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt[]{x+1}+1}=\dfrac{3}{2}\)
\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên hàm liên tục tại \(x=0\)
2b.
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x^2+2\right)\left(x-1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}\left(x^2+2\right)=3\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)=\lim\limits_{x\rightarrow1^+}\left(3x+a\right)=a+3\)
- Nếu \(a=0\Rightarrow f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)\) hàm liên tục tại \(x=1\)
- Nếu \(a\ne0\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow\) hàm không liên tục tại \(x=1\)
Hàm số: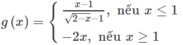
tại x = 1 có tập xác định là R
Ta có g(1) = -2 (1)
Từ (1), (2) và (3) suy ra
Vậy g(x) liên tục tại x = 1