Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a. $=2x(x-3)$
b. $=x^3(x+3)+(x+3)=(x^3+1)(x+3)=(x+1)(x^2-x+1)(x+3)$
c. $=64-(x^2-2xy+y^2)=8^2-(x-y)^2$
$=(8-x+y)(8+x-y)$
Bài 2:
$(x+5)(x+1)+(x-2)(x^2+2x+4)-x(x^2+x-2)$
$=x^2+6x+5+(x^3-2^3)-(x^3+x^2-2x)$
$=x^2+6x+5+x^3-8-x^3-x^2+2x$
$=8x-3$
Ta có đpcm.

Bài 2:
a: \(\Leftrightarrow4x^2-20x+25-4x^2+12x=0\)
=>-8x=-25
hay x=25/8
1.
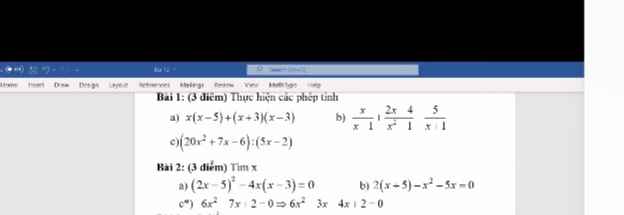
a) x (x - 5) + (x + 3)(x - 3)=
= x^2 - 5x + (x + 3)(x - 3)
= x^2 - 5x + x^2 - 9
= x^2 + x^2 - 5x - 9
= 2x^2 - 5x - 9.
b. không thể nhìn thấy hết bài được. Nó bị mất dấu!!
c. (20x^2 + 7x - 6) : (5x - 2)
= (5x - 2) (4x + 3) : (5x - 2)
= 4x + 3.
2.
a. (2x - 5)^2 - 4x (x - 3)= 0
-8x + 25= 0
-8x + 25 - 25= 0 - 25
-8x= -25
-8x : 8= -25 : 8
x = 25/8
Vậy x= 25/8
b. 2(x - 5) - x^2 - 5x= 0
-10x= 0
-10x : (-10)= 0 : (-10)
x= 0
Vậy x= 0
c. Lí do cũng giống câu b bài 1.

\(\frac{x}{3}=\frac{y}{4};\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{x}{15}=\frac{y}{20};\frac{y}{20}=\frac{z}{28}\Rightarrow\frac{x}{15}=\frac{x}{20}=\frac{z}{28}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{15}=\frac{y}{20}=\frac{z}{28}=\frac{2x+3y-z}{30+60-28}=\frac{186}{62}=3\)
suy ra :
\(\frac{x}{15}=3\Rightarrow x=45\)
\(\frac{y}{20}=3\Rightarrow y=60\)
\(\frac{z}{28}=3\Rightarrow z=84\)
ghi la de
Ta lấy 4 ; 5 là boi chug
BC(4,5)=20
\(\Rightarrow\frac{x}{3}=\frac{5y}{20};\frac{4y}{20}=\frac{z}{7}\Rightarrow\frac{x}{15}=\frac{y}{20};\frac{y}{20}=\frac{z}{28}\Rightarrow\frac{x}{15}=\frac{y}{20}=\frac{z}{28}\)
\(\frac{x}{3}=\frac{y}{20}=\frac{z}{7}\) va 2x +3y-z=186
\(\frac{x}{15}=\frac{y}{20}=\frac{z}{28}=\frac{2x}{30}=\frac{3y}{60}=\frac{z}{28}\)
\(\frac{2x}{30}=\frac{3y}{60}=\frac{z}{7}\) va 2x+3y-z=186
Áp dụng chất tỉ so bằng nhau ta có :
\(\frac{2x}{30}=\frac{3y}{60}=\frac{z}{28}=\frac{2x+3y-z}{30+60-28}=\frac{186}{62}=3\)
Suy ra :\(\frac{x}{15}=3\Rightarrow x=3.15=45\)
\(\frac{y}{20}=3\Rightarrow y=3.20=60\)
\(\frac{z}{28}=3\Rightarrow z=3.28=84\)
Vậy :................

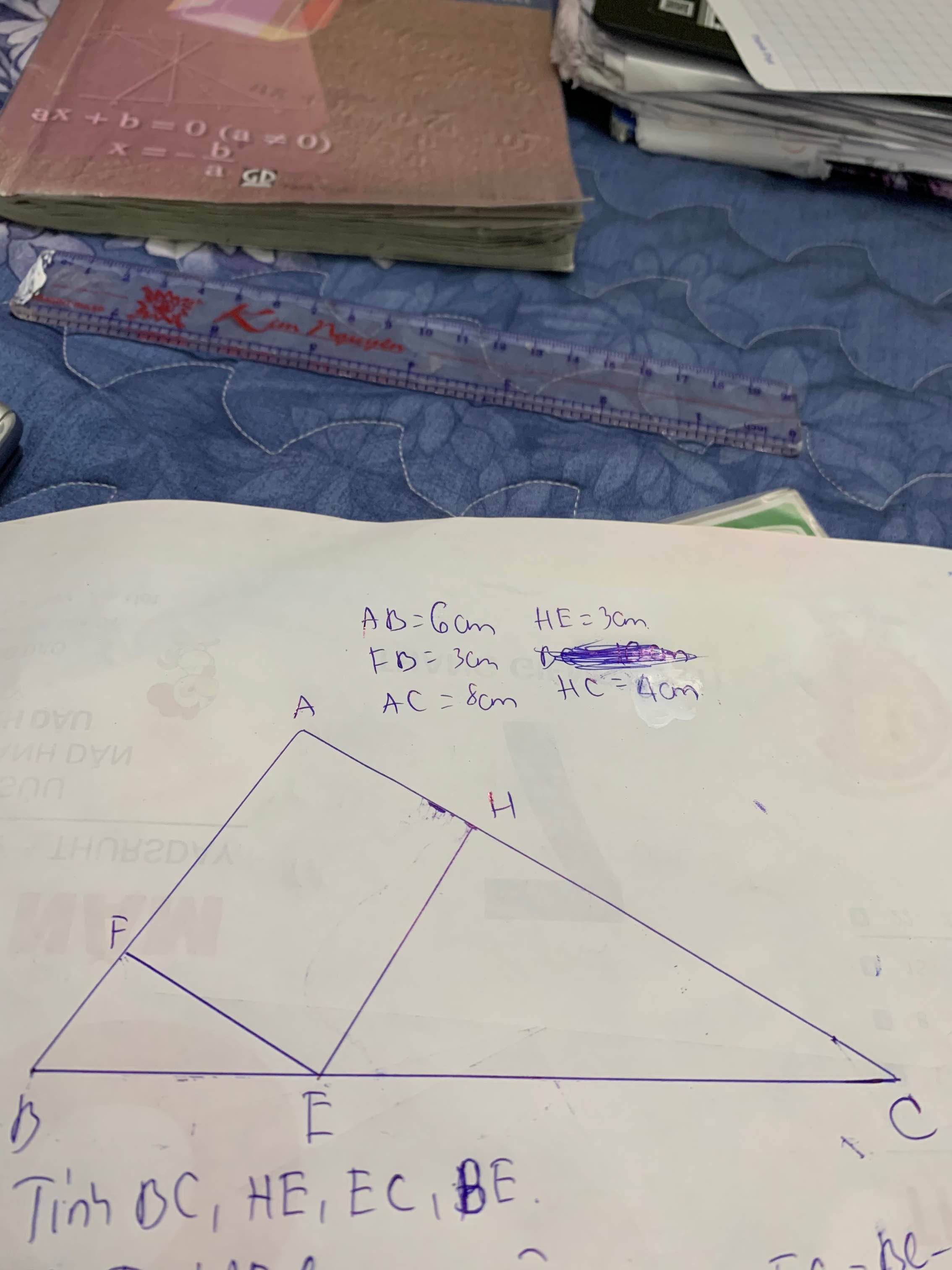
a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
b,c: góc FAE+góc FHE=180 độ
=>FAEH nội tiếp
=>góc HFE=góc HAE=góc C
Xét ΔHFE vuông tại H và ΔHCA vuông tại H có
góc HFE=góc HCA
=>ΔHFE đồng dạng với ΔHCA
=>HF/HC=HE/HA
=>HF*HA=HC*HE





Có : x^3-x^2+2x-8
= (x^3-2x^2)+(x^2-2x)+(4x-8)
= (x-2).(x^2+x+4)
Tk mk nha