Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C n 1 + C n 2 = 55
⇔ n ! n - 1 ! . 1 ! + n ! n - 2 ! . 2 ! = 55 ⇔ n + n . n - 1 2 = 55 ⇔ 2 n + n 2 - n = 110 ⇔ n = 10 n = - 11 l
x 3 + 2 x 2 n
= ∑ k = 0 10 . C 10 k . x 3 10 - k . 2 x 2 k = ∑ k = 0 10 . C 10 k . 2 k . x 30 - 3 k - 2 k
Số hạng không chứa x trong khai triển ⇒ tìm hệ số của số hạng chứa x 0 trong khai triển
⇒ x 30 - 3 k - 2 k = x 0 ⇔ k = 6
Vậy số hạng cần tính là C 10 6 . 2 6 = 13440
Đáp án cần chọn là D

Chọn đáp án D.

Số hạng này không chứa x khi và chỉ khi ![]()
Suy ra số hạng không chứa x trong khai triển trên là ![]()

Đáp án D.
Phương pháp
Sử dụng công thức C n k = n ! k ! n − k ! tìm n.
Sử dụng khai triển nhị thức Newton
a + b n = ∑ k = 0 n C n k . a n − k . b k
Cách giải
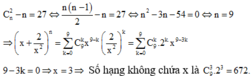
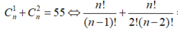
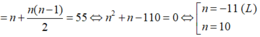

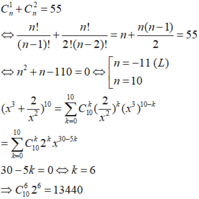
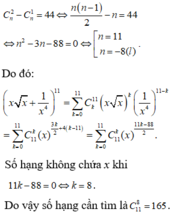
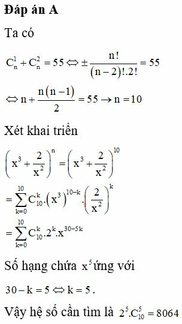
Đáp án D.
Ta có
C n 1 + C n 2 = 55 ⇔ n ! 1 ! n − 1 ! + n ! 2 ! n − 2 ! = 55 ⇔ n + 1 2 n n − 1 = 55 ⇔ n = 10 n = − 11 l
Khi đó
x 3 + 2 x 2 n = x 3 + 2 x 2 10 = ∑ n = 0 10 C 10 n x 3 n 2 x 2 10 − n = ∑ n = 0 10 C 10 n 2 10 − n x 5 n − 20
Số hạng không chưa x khi 5 n − 20 = 0 ⇔ n = 4 ⇒ n = 4 ⇒ số hạng không chứa x là C 10 4 .2 10 − 4 = 13440.