Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Muốn cho một hàm số là hàm số bậc nhất thì nó phải có dạng y = ax + b, với a \(\ne\) 0. Do đó:
a) Điều kiện là: \(\sqrt{5-m}\ne0\) hay 5 - m > 0. Suy ra m < 5.
b) Điều kiện là: \(\dfrac{m+1}{m-1}\ne0\) hay m + 1 \(\ne\)0, m - 1 \(\ne\)0. Suy ra m \(\ne\pm1\)
a) Để hàm số y= \(\sqrt{5-m}\) (x-1) là bậc nhất:
ta có: a\(\ne\) 0 \(\Rightarrow\) \(\sqrt{5-m}\) \(\ne\) 0 \(\Rightarrow\) 5 - m > 0 \(\Rightarrow\) m < 5.
Vậy : m<5 thì hàm số y= \(\sqrt{5-m}\)(x - 1) là bấc nhất.
b) Để hàm số \(y=\dfrac{m+1}{m-1}x+3,5\) là bậc nhất:
ta có : a\(\ne0\) \(\Rightarrow\) \(\dfrac{m+1}{m-1}\ne0\Rightarrow\) m+1 \(\ne0,m-1\ne0\Rightarrow m\ne\pm1\)
Vậy: \(m\ne\pm1\) thì hàm số \(y=\dfrac{m+1}{m-1}x+3,5\) là bậc nhất.

Hàm là bậc nhất khi:
a. \(3m-2\ne0\Rightarrow m\ne\dfrac{2}{3}\)
b. \(3-m>0\Rightarrow m< 3\)
c. \(\left\{{}\begin{matrix}2m-1\ne0\\m+2\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\m\ne-2\end{matrix}\right.\)
d. \(\left\{{}\begin{matrix}m^2-4=0\\m+2\ne0\end{matrix}\right.\) \(\Rightarrow m=2\)
a: ĐKXĐ: \(m\ne\dfrac{2}{3}\)
b: ĐKXĐ: \(m< 3\)
c: ĐKXĐ: \(\left[{}\begin{matrix}m\ge\dfrac{1}{2}\\m< -2\end{matrix}\right.\)
d: ĐKXĐ: \(m=2\)

\(a,\Leftrightarrow\dfrac{m-1}{m+1}\ne0\Leftrightarrow m\ne\pm1\\ b,\Leftrightarrow\dfrac{m-1}{m+1}>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\\ c,\Leftrightarrow\dfrac{m-1}{m+1}+m+2=2\\ \Leftrightarrow\dfrac{m-1+m^2+m}{m+1}=0\\ \Leftrightarrow m^2+2m-1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt{2}\\m=-1-\sqrt{2}\end{matrix}\right.\)

Hàm số \(y=\sqrt{3-m}\left(x+5\right)\) là hàm số bậc nhất khi \(\sqrt{3-m}\ne0\)
\(\Leftrightarrow3-m\ne0\)
\(\Leftrightarrow m\ne3\)
Tọa độ giao điểm của hai đồ thị hàm số \(y=\dfrac{1}{2}x-2\) và \(y=\dfrac{3}{2}x-2\) là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x-2=\dfrac{3}{2}x-2\\y=\dfrac{1}{2}x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}x-2-\dfrac{3}{2}x+2=0\\y=\dfrac{1}{2}x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=0\\y=\dfrac{1}{2}x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\cdot0-2=-2\end{matrix}\right.\)
Vậy: Hai đồ thị hàm số \(y=\dfrac{1}{2}x-2\) và \(y=\dfrac{3}{2}x-2\) có tọa độ giao điểm là (0;-2)
\(y=\sqrt{3-m}.\left(x+5\right)\) là hàm số bậc nhất \(\Leftrightarrow\sqrt{3-m}\ne0\Leftrightarrow m\ne3\)
Lập PT hoành độ ta có:
\(\dfrac{1}{2}x-2=\dfrac{3}{2}x-2\)
\(\Leftrightarrow x=0\)
\(\Rightarrow y=\dfrac{1}{2}.0-2=-2\)
=> Tọa độ (0;-2)

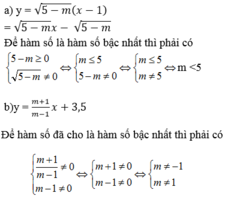
a: ĐKXĐ: \(m\le5\)
b: ĐKXĐ: \(m\notin\left\{-1;1\right\}\)
c: ĐKXĐ: \(m\ne-2\)