Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A là abc thì B=abc.1000+abc
Theo đề bài ta có
(abc.1000+abc):7:11:13=abc
abc(1000+1)=abc.1001
abc(1000+1)=abc.1001
Vậy đó mình giải thích xong rồi suy ra B:7:11:13=A
Tk mk

Ta gọi số A là abc
Gọi số B là abcabc
Ta có : abcabc : 7 : 11 : 13 = abc
Mà abcabc : abc = 1001 hay abcabc : 1001 = abc
Vì abcabc : (7 . 11 . 13) = abc
abcabc : 1001 = abc
Vậy số B : 7 : 11 : 13 = số A
K CHO MIK NHA ><

Gọi A là abc thì B=abc.1000+abc
Theo đề bài ta có
(abc.1000+abc):7:11:13=abc
abc(1000+1)=abc.1001
abc(1000+1)=abc.1001
Vậy đó mình giải thích xong rồi suy ra
B:7:11:13=A

Mình có cách phân tích khác nhé : ![]()
Gọi A là \(\overline{abc}\) thì ta được : B = \(\overline{abc}.1000+\overline{abc}\)
Theo bài ra ta có :
\(\left(\overline{abc}.1000+\overline{abc}\right):7:11:13=\overline{abc}\)
\(\overline{abc}\left(1000+1\right)=\overline{abc}.7.11.13\)
\(\overline{abc}.1001=\overline{abc}.1001\)
(A=overline{abc}), (B=overline{abcabc}).Ta có:
(overline{abc}).7.11.13=(overline{abc}).1001=(overline{abcabc}) nên
(overline{abcabc}):7:11:13=(overline{abc})

Giả sử A là abc¯abc¯
=> B=abcabc¯B=abcabc¯
Ta có
abc¯.1001=abcabc¯abc¯.1001=abcabc¯
=> abc¯=abcabc¯:1001abc¯=abcabc¯:1001 (1)
Mặt khác
Giải giả thiết ta được
abcabc¯:7:11:13=abc¯abcabc¯:7:11:13=abc¯
=> abcabc¯:(7.11.13)=abc¯abcabc¯:(7.11.13)=abc¯
=> abcabc¯:1001=abc¯abcabc¯:1001=abc¯
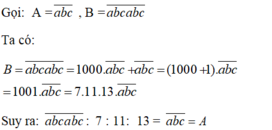
A = abc
B = abcabc
1/
{[(abcabc:7):11]:13}
= (abcabc) : (7*11*13)
= abcabc : 1001
Thí dụ một số bất kỳ có dạng abcabc:
123123 = (123 * 1000) + 123 = 123123
539539 = (539 * 1000) + 539 = 539539
Suy ra:
2/
abcabc = (abc * 1000) + abc
= abc * (1000 + 1)
= abc * 1001
Thay kết quả 2/ vào 1/
abcabc : 1001 = (abc * 1001) : 1001 = abc
A = abc
B = abcabc
1/
{[(abcabc:7):11]:13}
= (abcabc) : (7*11*13)
= abcabc : 1001
Thí dụ một số bất kỳ có dạng abcabc:
123123 = (123 * 1000) + 123 = 123123
539539 = (539 * 1000) + 539 = 539539
Suy ra:
2/
abcabc = (abc * 1000) + abc
= abc * (1000 + 1)
= abc * 1001
Thay kết quả 2/ vào 1/
abcabc : 1001 = (abc * 1001) : 1001 = abc