Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cũng được gọi là đa thức 
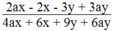xác định khi 4ax + 6x + 9y + 6ay
≠
0
⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0
Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y
Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2
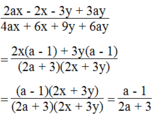
Vậy biểu thức không phụ thuộc vào x, y.
xác định khi:
(x + y)(6x – 6y)
≠
0 ⇒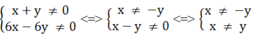 
Điều kiện x ≠ ± y
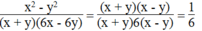
Vậy biểu thức không phụ thuộc vào x, y.
Ta có: 3x + y = 1 => y = 1 - 3x
a, Thay y = 1 - 3x vào M, ta có:
\(\Rightarrow M=3x^2+\left(1-3x\right)^2=3x^2+1-6x+9x^2=12x^2-6x+1=3\left(4x^2-2x+\frac{1}{3}\right)\)
\(=3\left(4x^2-2x+\frac{1}{4}+\frac{1}{12}\right)=3\left(2x-\frac{1}{2}\right)^2+\frac{3}{12}=3\left(2x-\frac{1}{2}\right)^2+\frac{1}{4}\)
Vì \(\left(2x-\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow3\left(2x-\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow3\left(2x-\frac{1}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}\forall x\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}2x-\frac{1}{2}=0\\3x+y=1\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x=\frac{1}{4}\\y=1-3x=1-3.\frac{1}{4}=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow x=y=\frac{1}{4}\)
Vậy GTNN M = 1/4 khi x = y = 1/4
b, Thay y = 1 - 3x vào N
\(\Rightarrow N=x\left(1-3x\right)=x-3x^2=-3\left(x^2-\frac{x}{3}+\frac{1}{36}-\frac{1}{36}\right)\)
\(=-3\left(x-\frac{1}{6}\right)^2-3.\left(-\frac{1}{36}\right)=-3\left(x-\frac{1}{6}\right)^2+\frac{1}{12}\)
Vì \(\left(x-\frac{1}{6}\right)^2\ge0\forall x\)
\(\Rightarrow-3\left(x-\frac{1}{6}\right)^2\le0\forall x\)
\(\Rightarrow-3\left(x-\frac{1}{6}\right)^2+\frac{1}{12}\le\frac{1}{12}\forall x\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}x-\frac{1}{6}=0\\3x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{6}\\y=1-3x=1-3.\frac{1}{6}=\frac{1}{2}\end{cases}}\)
Vậy GTLN N = 1/12 khi x = 1/6 và y = 1/2
a) Vì mỗi đơn thức là một đa thức nên ta có thể viết bất kỳ đơn thức nào ở câu này.
Ví dụ: P(x) = xy2 (Vì đơn thức cũng là một đa thức)
b) Có vô số đa thức không phải là đơn thức.
Ví dụ: 2x + 3y; x2 + 2y