Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
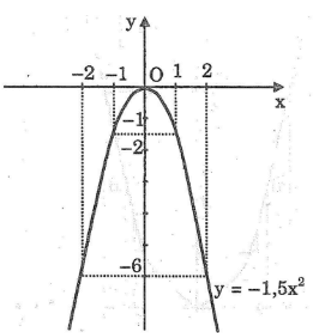
b: Vì a=-1,5<0 nên hàm số đồng biến khi x<0 và nghịch biến khi x>0
=>f(-1,5)< f(-0,5) và f(0,75)>f(1,5)
- Khi 1 ≤ x ≤ 2 thì -6 ≤ y ≤ -1,5 ;
- Khi -2 ≤ x ≤ 0 thì -6 ≤ y ≤ 0 ;
- Khi -2 ≤ x ≤ 1 thì -6 ≤ y ≤ 0.

\(a,\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}=\dfrac{x^2+x+1+1}{\sqrt{x^2+x+1}}=\sqrt{x^2+x+1}+\dfrac{1}{\sqrt{x^2+x+1}}\left(1\right)\)
Áp dụng BĐT cosi: \(\left(1\right)\ge2\sqrt{\sqrt{x^2+x+1}\cdot\dfrac{1}{\sqrt{x^2+x+1}}}=2\)
Dấu \("="\Leftrightarrow x^2+x+1=1\Leftrightarrow x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2

b: Vì (Δ)//(d) nên m=-2
Vậy: (Δ): y=-2x+n
Phương trình hoành độ giao điểm là
\(-\dfrac{1}{2}x^2+x-n=0\)
\(\text{Δ}=1^2-4\cdot\dfrac{-1}{2}\cdot\left(-n\right)=1-2n\)
Để (d) tiếp xúc với (P) thì -2n+1=0
hay n=1/2