Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Số các số tự nhiên thỏa mãn yêu cầu bài toán là: A 6 4 = 360 số

Đáp án B
Số cần lập là a b c d e f ¯ , ta có a + b + c − 1 = d + e + f ⇔ 20 = 2 d + e + f ⇔ d + e + f = 10
Với mỗi f ∈ 1 ; 3 ; 5 ⇒ d , e có 4 cách chọn, suy ra a b c d e f ¯ có 4.3 ! = 24 cách chọn
Suy ra có 3.24 = 72 số có thể lập thỏa mãn đề bài

Chọn đáp án A.
Xếp một hàng thành 6 ô đánh số từ 1 đến 6 như hình bên: 123456.
Số các chữ số gồm 6 chữ số khác nhau được lập từ 6 chữ số đã cho là 5.5! = 600 số.
Ta tìm số các chữ số mà hai chữ số 0 và 5 đứng cạnh nhau:
· Chữ số 0 và 5 cạnh nhau tại ô số 1 và 2 có 1.4! = 24 số.
· Chữ số 0 và 5 đứng cạnh nhau tại các ô (2;3), (3;4), (4;5), (5;6) có 4.2!.4! = 192 số.
Vậy có tất cả 24 + 192 = 216 số mà chữ số 0 và 5 đứng cạnh nhau.
Do đó, số các số thỏa mãn yêu cầu bài toán là 600 – 216 = 384 số.

Đáp án C
Trước tiên ta đếm số các số lẻ có bốn chữ số đôi một khác nhau lập được từ các số đã cho: có 3 cách chọn chữ số hàng đơn vị, có 4 cách chọn chữ số hàng nghìn, có A 4 2 = 6 . 2 cách chọn hai chữ số hàng trăm và hàng chục. Như vậy có 3.4.6.2=144 số như trên.
Tiếp theo ta đếm số các số lẻ có bốn chữ số đôi một khác nhau và không có mặt chữ số 1: Tương tự trường hợp trên, ta được số các số thuộc loại này là: 2.3.3=18.
Vậy số các số tự nhiên lẻ có bốn chữ số đôi một khác nhau mà phải có mặt số 1 là: 144 - 18 = 126

Chọn đáp án B
Phương pháp
Số các số lập được chính là số hoán vị của 4.
Cách giải
Mỗi số lập được thỏa mãn bài toán là một hoán vị của 4 chữ số 1; 5; 6; 7.
Số các số có bốn chữ số đôi một khác nhau lập được từ 4 chữ số 1; 5; 6; 7 là 4!=24 số.


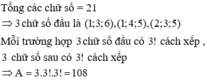

Đáp án B
Số các số có thể lập được bằng 5.4.3 = 60 số