Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P ( A ) = 1 8 + 1 16 = 3 16 .
Không gian mẫu là kết quả của việc sắp xếp 10 người theo 1 thứ tự.
⇒ n(Ω) = P10 = 10! = 3 628 800.
a) Gọi M: “A và B đứng liền nhau”
* Coi A và B là một phần tử X.
Số cách xếp X và 8 người khác thành hàng dọc là: 9!
Số cách xếp hai người A và B là: 2!= 2 cách
Theo quy tắc nhân có: 9!.2= 725760 cách xếp thỏa mãn
Xác suất của biến cố M là: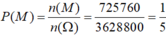 
b) Gọi N: “Trong hai người đó có một người đứng ở vị trí số 1 và một người kia đứng ở vị trí cuối cùng”.
+ Sắp xếp vị trí cho A và B: Có 2 cách
+ Sắp xếp vị trí cho 8 người còn lại: có 8! cách
⇒ Theo quy tắc nhân: n(N) = 2.8!
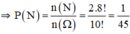
Gọi A là biến cố cầu thủ thứ nhất ghi bàn
B là biến cố cầu thủ thứ hai ghi bàn
X là biến cố ít nhất 1 trong hai cầu thủ ghi bàn
Suy ra: X ¯ = A ¯ . B ¯
Vì hai biến cố A ¯ ; B ¯ độc lập với nhau nên ta có:
P ( X ¯ ) = P ( A ¯ ) . P ( B ¯ ) = ( 1 − 0 , 8 ) . ( 1 − 0 , 7 ) = 0 , 06
Do đó, xác suất để có ít nhất 1 trong hai cầu thủ ghi bàn là:
P ( X ) = 1 − P ( X ¯ ) = 1 − 0 , 06 = 0 , 94
Chọn đáp án B
Chọn A
Có 
cách chia 20 bạn vào 4 nhóm, mỗi nhóm 5 bạn.
- Gọi A là biến cố “ 5 bạn nữ vào cùng một nhóm”
- Xét 5 bạn nữ thuộc nhóm A có 
cách chia các bạn nam vào các nhóm còn lại.
- Do vai trò các nhóm như nhau nên có 
Khi đó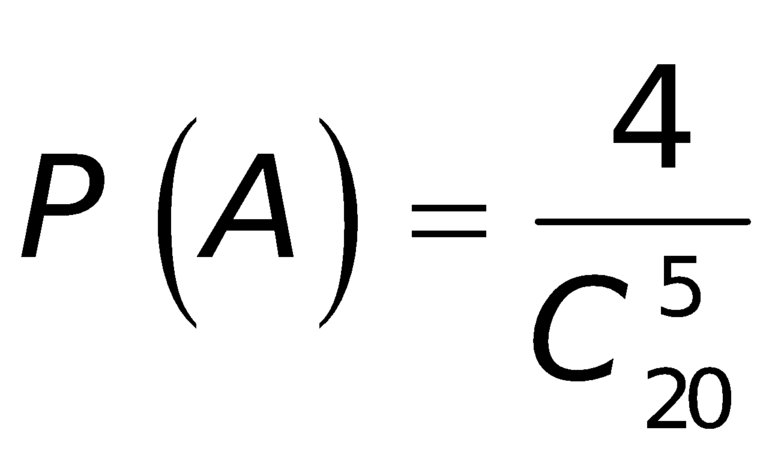 
.
Mỗi lần quay bánh xe dừng lại ở 1 trong 7 vị trí: n(Ω) = 73=343.
Trong 3 lần quay kim của bánh xe lần lượt dừng lại ở 3 vị trí khác nhau nên ta có : n(X) = \(A^3_7\)= 210.
=> Xác xuất của 3 lần quay là: P=\(\dfrac{n\left(X\right)}{n\left(\Omega\right)}\)=\(\dfrac{30}{49}\)
Những trận đấu giữa Real Madrid và Barcelona luôn rất rất căng thẳng và đỉnh điểm chính là trong giai đoạn 1953-1966 và 2010-2013