

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Số vân sáng trong khoảng MN chính là số k thỏa mãn
\(x_M < x_s < x_N\)
=> \( 2 < k i < 4,5 \)
=> \(1,67 < k < 3,75.\)
Do \(k \in Z \) => \( k = 2,3.\)
Tương tự.
Số vân tối trong khoảng MN chính là số k thỏa mãn
\(x_M < x_t < x_N\)
=> \( 2 < (k+\frac{1}{2})i < 4,5\)
=> \( 1,167 < k < 3,25.\)
Do \(k \in Z \) => \(k = 2,3.\)
Vẫn chưa hiểu tại đoạn: k∈Z => k=2,3. Ai giải thích cho mình với ạ.

\(i = \frac{\lambda D}{a}= \frac{0,6.2,5}{1}=1,5 mm.\)
Số vân sáng quan sát trên màn
\(N_s = 2.[\frac{L}{2i}]+1=2.4+1 = 9.\)
Số vân tối quan sát trên màn
\(N_t = 2[\frac{L}{2i}+0,5]=2.4 = 8.\)
Tổng số vân sáng và vân tối là
\(N = N_t + N_s = 9+8 = 17.\)

Chọn đáp án A
? Lời giải:
+ i 2 = λ D 2 a = 750.10 − 6 .2.10 3 2.1 , 5 = 0 , 5 m m

Đáp án D
Khoảng vân 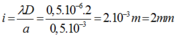
*Khoảng cách giữa một vân sáng và một vân tối cạnh nhau được tính bởi
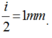 .
.

Phương pháp
Áp dụng công thức tính khoảng vân trong giao thoa sóng ánh sáng
Cách giải:
ta có khoảng vân i = λ D a
khoảng cách giữa một vân sáng và một vân tối trong giao thoa sóng ánh sáng sáng là một nửa khoảng vân = 1mm
=> Chọn D