Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
+ Điều kiện để có sự trùng nhau của hai hệ vân sáng
.
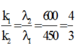
Xét tỉ số
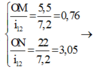có 3 vân trùng.
Chọn C
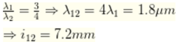
Vậy trên đoạn MN có 3 vị trí vân sáng trùng nhau (7.2, 14.4, 21.6)
Đáp án C
+ Khoảng vân giao thoa của hai bức xạ
;
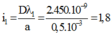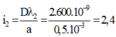
+ Các vị trí hệ hai vân sangs trùng nhau
mm cứ sau mỗi khoảng
lại có một vị trí trùng nhau của hệ hai vân sang.
Xét tỉ số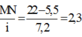 
=> có hai vân sáng trùng nhau.
Trong thí nghiệm Y-âng về giao thoa ánh Sáng, khoảng cách giữa hai khe là 0,5 mm, khoảng cách từ hai khe đến màn quan Sát là 2m. Nguồn Sáng dùng trong thí nghiệm gồm hai bức xạ có bước Sóng lamda1 =0,450 miromet và lamda2 = 0,60 miromet. Trên màn quan Sát, gọi M, N là hai điểm ở cùng một phía so với vân trung tâm và cách vân trung tâm lần lượt là 6,5 mm và 20 mm. Trên đoạn MN, Số vị trí vân Sáng trùng nhau của hai bức xạ là
A. 4. B. 2. C. 5. D. 3.
==> tọa độ các vân trùng (so với vân trung tâm) x = k.4i1 = 7,2k với k = 0,1,2. . .
Ta có: OM <= x = 7,2k <= ON ==> 0,9 <= k <= 2,78 ==> có hai vị trí
Đổi đơn vị: \(\lambda_1=450n m= 0,45 \mu m.\)
\(\lambda_1=600n m= 0,6 \mu m.\)
Hai vân sáng trùng nhau khi \(k_1i_1=k_2i_2 \)
<=> \(\frac{k_1}{k_2}= \frac{i_1}{i_2}=>\frac{k_1}{k_2}= \frac{\lambda_1}{\lambda_2} =\frac{3}{4}\ \ (*)\)
Xét trong đoạn MN nên \(5,5 mm \leq x_s \leq 22mm. \)
<=> \(5,5 mm \leq k_1\frac{\lambda_1 D}{a} \leq 22mm. \)
<=> \(\frac{5,5.a}{\lambda_1 D} \leq k_1\leq \frac{22.a}{\lambda_1 D}\)
Giữ nguyên đơn vị của a = 0,5 mm; D = 2m; \(\lambda_1=0,45 \mu m.\)
<=> \(3,055 \leq k_1 \leq 12,22\)
Kết hợp với (*) ta có \(k_1\) chỉ có thể nhận giá trị : 3x2= 6; 3x3 = 9; 3x4 =12.
Như vậy có 3 vị trí trùng nhau của hai bức xạ trong đoạn MN.
Đáp án D
Phương pháp: Coi sự giao thoa trùng vân giống như giao thoa ánh sáng đơn sắc, ta đi tìm khoảng vân trùng nhau.
Cách giải:
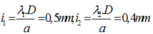
Vị trí vân sáng và vân tối thỏa mãn điều kiện :
Vì vân sáng trùng với vị trí vân tối nên ta có:
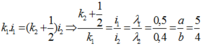
Coi đây là hiện tượng giao thoa với khoảng vân trùng nhau là:
Số vân trùng nhau trong khoảng MN thỏa mãn điều kiện :
Vậy có 15 giá trị k thỏa mãn
Phương pháp:
Sử dụng lí thuyết về bài toán trùng nhau của 2 bức xạ trong giao thoa sóng ánh sáng
Hai bức xạ trùng nhau: x1 = x2 <=> k1.λ1 = k2.λ2
Cách giải:
+ Ta có: i1 = 0,6 mm và i2 = 0,78 mm
+ Vị trí hai bức xạ trùng nhau:
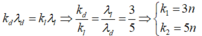
+ Số vân sáng của λ 1 = 500 nm trên đoạn MN là:
có 10 giá trị
+ Số vân sáng của λ 2 = 650 nm trên đoạn MN là:
có 8 giá trị
+ Số vân sáng trùng của hai bức xạ trên đoạn MN là:
có 1 giá trị
+ Số vân sáng quan sát được là: N = N1 + N2 – N0 = 17
Chọn B
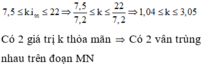
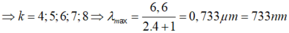
Đáp án D