Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

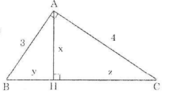
ΔABC vuông tại A có AB = 3, AC = 4 và đường cao AH như trên hình.
Theo định lí Pitago ta có:
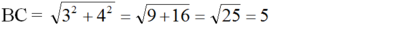
Mặt khác, AB2 = BH.BC (định lí 1)
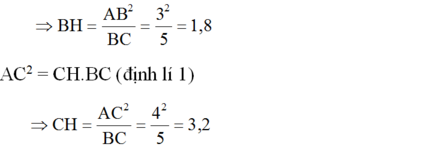
Theo định lí 3 ta có: AH.BC = AB.AC
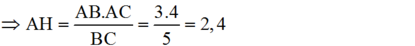

Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)

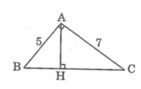
Giả sử tam giác ABC có ![]() , AB = 5, AC = 7
, AB = 5, AC = 7
Theo định lí Pi-ta-go, ta có:
B C 2 = A B 2 + A C 2
⇒ BC = ![]()
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
AH.BC = AB.AC ⇒ AH = ![]()
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
A
B
2
=
B
H
.
B
C
⇒ BH = 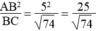
CH = BC – BH = 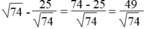

Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=7^2+24^2=625\)
hay BC=25(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có HA là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=6.72\left(cm\right)\\BH=1.96\left(cm\right)\\CH=23.04\left(cm\right)\end{matrix}\right.\)

ΔABC vuông tại A có AB = 3, AC = 4 và đường cao AH như trên hình.
Theo định lí Pitago ta có:
Mặt khác, A B 2 = B H . B C (định lí 1)
Theo định lí 3 ta có: AH.BC = AB.AC