Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số ghế trong phòng học là x (ghế), số học sinh của lớp là y (học sinh). Điều kiện x, y ∈N*
Nếu xếp mỗi ghế 3 học sinh thì 6 học sinh không có chỗ, ta có phương trình: 3x + 6 = y
Nếu xếp mỗi ghế 4 học sinh thì thừa một ghế, ta có phương trình: (x – 1)4=y
Ta có hệ phương trình:
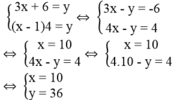
Giá trị của x và y thỏa điều kiện bài toán.
Vậy trong phòng học có 10 ghế và 36 học sinh.

gọi số học sinh là x(hs;x∈N*)
số ghế dài là y(ghế;y∈N*)
vì khi xếp mỗi ghế 3 học sinh thì 6 học sinh không có ghế ngồi
nên ta có phương trình x -3y = 6(1)
vì xếp mỗi ghế 4 học sinh thì thừa 1 ghế
ta có pt x = 4(y-1)
<=> x - 4y = -4(2)
từ (1)(2)ta có hpt
x-3y=6 và x-4y = -4 <=> x =36 ; y=10(tm)

Gọi số người dự họp và số ghế có trong phòng lần lượt là \(a,b\)(\(a,b\inℕ\))
Theo bài ra ta có hệ phương trình: \(\hept{\begin{cases}a=5b+9\\a=6b-1\end{cases}}\Leftrightarrow\hept{\begin{cases}a=59\\b=10\end{cases}}\)(thỏa mãn)

Đặt số ghế là x; số học sinh là y ta có hệ phương trình
\(\hept{\begin{cases}4x=y-6\\\frac{y}{5}=x-1\end{cases}}\)
Bạn tự giải nốt hệ nhé

Gọi số ghế và số học sinh của lớp lần lượt là \(x,y\left(x,y\inℕ^∗\right)\)
Nếu xếp mỗi ghế 4 học sinh thì 7 học sinh không có chổ, vì vậy ta có phương trình \(4x+7=y\)\(\Leftrightarrow y-4x=7\)(1)
Nếu xếp mỗi ghế 5 học sinh thì còn thừa 1 ghế, nên ta có phương trình \(\frac{y}{5}+1=x\Leftrightarrow y+5=5x\Leftrightarrow5x-y=5\)(2)
Từ (1) và (2) ta có hệ phương trình \(\hept{\begin{cases}y-4x=7\\5x-y=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=4x+7\\5x-\left(4x+7\right)=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=4x+7\\x=12\left(nhận\right)\end{cases}}\Leftrightarrow\hept{\begin{cases}y=55\left(nhận\right)\\x=12\end{cases}}\)
Vậy lớp có 12 ghế và 55 học sinh.

Lời giải:
Giả sử trong phòng học có $a$ học sinh.
Theo bài ra, nếu xếp mỗi bộ bàn ghế 3 hs thì số bộ bàn ghế là:
$\frac{a-4}{3}$ (bộ)
Nếu xếp mỗi bộ bàn ghế 4 học sinh thì số bộ bàn ghế là:
$\frac{a-2}{4}$ (bộ)
Số bộ bàn ghế không đổi nên: $\frac{a-4}{3}=\frac{a-2}{4}$
$\Rightarrow a=10$ (hs)
Số bộ bàn ghế là: $\frac{a-2}{4}=\frac{10-2}{4}=2$ (bộ)