Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là C 12 3 = 220
b. Gọi B là biến cố :” trong 3 người được chọn không có cặp vợ chồng nào” thì B ¯ là biến cố :” có đúng một cặp vợ chồng trong ba người được chọn”
![]()
( vì có 3 cách chọn cặp vợ chồng, và 10 cách chọn người thứ 3 trong số 10 người còn lại) nên
![]()
Chọn D

Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là C_123= 220
a. Gọi A là biến cố:” trong 3 người được chọn có đúng 1 nam”
n(A)= C61. C62= 90. Do đó P(A) =90/220=9/22
Chọn B

Chọn B
Gọi 2 cặp vợ chồng là C1-V1 và C2-V2 (C=chồng, V=vợ).
* Số cách chọn ra 7 đôi:
- Đầu tiên chọn ra 7 nam trong 10 nam: C 10 7 (cách).
- Xếp 7 người nam này thành 1 hàng ngang, người đầu tiên có 12 cách ghép với nữ, người thứ hai có 11 cách, cứ như thế suy ra số cách ghép đôi là 12.11.10.9.8.7.6 (cách).
- Theo quy tắc nhân có 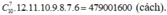
* Số cách chọn 7 đôi, chỉ có một cặp vợ chồng
- Trường hợp 1: chỉ có cặp vợ chồng C1-V1, khi đó lấy 6 nam trong 9 nam còn lại:
+ Nếu trong 6 nam này không có C2 thì số cách ghép 6 cặp còn lại là: ![]()
+ Nếu trong 6 nam này có C2 thì số cách ghép 6 cặp còn lại là: có 10 cách ghép C2 với nữ (trừ V2 và trừ V1), 5 nam còn lại có cách, số cách ghép cặp cho 5 nam này là 10.9.8.7.6 cách. Vậy theo quy tắc nhân có ![]()
Theo quy tắc cộng, có ![]()
- Trường hợp 2: chỉ có cặp vợ chồng C2-V2, tương tự như trên có 26248320(cách)
Vậy xác suất cần tính là: ![]()

a) Có 10 cách chọn ngờiđànông. Khi đã chọn người đàn ông rồi, chỉ có 1 cách chọn người đàn bà là vợ của người đàn ông đó. Vậy có 10 cách.
b) Có 10 cách chọn người đàn ông. Khi đã chọn người đàn ông rồi, có 9 cách chọn người đàn bà không là vợ của người đàn ông đó. Vậy có 10 × 9 = 90 cách chọn.

Để chọn một người đàn ông và một người phụ nữ không là vợ chồng, ta có
Có 10 cách chọn người đàn ông.
Có 9 cách chọn người phụ nữ ( trừ 1 người là vợ của người đàn ông đã chọn trước đó).
Vậy theo qui tắc nhân ta có 10.9 = 90 cách.
Chọn đáp án D.

câu 1) đặc các cặp vợ chồng lần lược là : \(A_1B_1;A_2B_2;A_3B_3....;A_{19}B_{19};A_{20}B_{20}\)
ta có : + số cách để chọn ra 4 người trong \(40\) người là : \(C^4_{40}\)
+ số cách để chọn ra 4 người mà không có cặp vợ chồng nào gồm
* cách chọn 4 người từ 20 người chồng là : \(C^4_{20}\)
* cách chọn 4 người từ 20 người vợ là : \(C^4_{20}\)
* số cách trộn lộn sộn đc tính như sau :
đặc 4 người đc chọn là : \(ABCD\)
\(\Rightarrow\) - \(A\) có 20 cách chọn
- \(B\) có 18 cách chọn
- \(C\) có 16 cách chọn
- \(D\) có 14 cách chọn
\(\Rightarrow\) có \(20.18.16.14=80640\) cách chọn
\(===\Rightarrow\) tổng cách chọn 4 người mà không có cặp vợ chồng nào là
\(C^4_{20}+C^4_{20}+80640\)
\(\Rightarrow\) sác xuất để chọn ra 4 người mà không có cặp vợ chồng nào là : \(P=\dfrac{C^4_{20}+C^4_{20}+80640}{C^4_{40}}=\dfrac{9033}{9139}\)
vậy .............................................................................................................................
câu còn lại để chiều về mk lm cho nha :)
mk lm câu còn lại như lời hứa nha
câu 2 )
+ số cách chọn 5 người từ 22 người là : \(C^5_{22}\)
+ cách chọn ra 5 người nhưng không có cặp vợ chồng nào đc tác ra 5 trường hợp
ta đặc : các giáo viên nam lần lược là : \(A_1;A_2...;A_9\)
các giáo viên nữ lần lược là : \(B_1;B_2...;B_{13}\)
trong đó \(A_1;B_1vàA_2;B_2\) là 2 cặp vợ chồng
gọi các người được chọn là \(A;B;C;D;E\)
* th1: chọn 5 người đều là nam có : \(C^5_9\) cách
* th2: chọn 5 người đều là nữ có : \(C^5_{13}\)
* th3: \(A\in\left\{A_1;B_1;A_2;B_2\right\}\)
\(\Rightarrow\) \(A\) có 4 cách chọn ; và số cách chọn 4 người \(B;C;D;E\) từ 18 người còn lại là \(C^4_{18}\)
mà trường hợp này lại bao gồm số cách chọn 5 người cùng giới
\(\Rightarrow\) có \(10827\) cách chọn
* th4: \(A;B\in\left\{A_1;B_1;A_2;B_2\right\}\)
\(\Rightarrow\) \(A\) có 4 cách chọn ; \(B\) có 2 cách chọn ; và số cách chọn 3 người \(C;D;E\) từ 18 người còn lại là \(C^3_{18}\)
mà trường hợp này cũng bao gồm số cách chọn 5 người cùng giới
\(\Rightarrow\) có \(5115\) cách chọn
* th5: \(A;B;C;D;E\notin\left\{A_1;B_1;A_2;B_2\right\}\)
\(\Rightarrow\) số cách chọn \(5\) người \(A;B;C;D;E\) từ 18 người còn lại là \(C^5_{18}\)
mà trường hợp này cũng gồm trường hợp chọn phải 5 người cùng giới ; nhưng số cách chọn 5 người cùng giới ở trường hợp này đã giảm xuống còn \(C^5_7+C^5_{11}=483\) cách
\(\Rightarrow\) có \(8085\) cách chọn
\(===\Rightarrow\) sác xuất để chọn ra 5 người trong 22 người đó nhưng không có cặp vợ chồng nào là : \(P=\dfrac{C^5_9+C^5_{13}+10827+5115+8085}{C^5_{22}}=\dfrac{4240}{4389}\)

Lời giải:
Gọi $A$ là biến cố chồng xem chương trình T, $B$ là biến cố vợ xem chương trình T
Theo bài ra: $P(A)=0,4; P(B)=0,5; P(A|B)=0,7$
a. Xác suất cả vợ và cả chồng xem T là:
$P(AB)=P(A|B)P(B)=0,7.0,5=0,35$
b. \(P(B|A)=\frac{P(AB)}{P(A)}=\frac{0,35}{0,4}=0,875\)
c. Xác suất ít nhất 1 trong 2 người xem:
\(P(AB)+P(A\overline{B})+P(\overline{A}B)=P(AB)+P(A)-P(AB)+P(B)-P(AB)\)
\(=P(A)+P(B)-P(AB)=0,4+0,5-0,35=0,55\)
Đề bài là chồng xem, biết vợ, v thì phải P(B|A) = 0.7 chứ sao lại P(A|B) cô?
\(n\left(\Omega\right)=C^3_{20}\)
A: "3 người được chọn ko có cặp vợ chồng nào"
=>\(\overline{A}\): 3 người được chọn có 1 cặp vợ chồng
=>\(n\left(\overline{A}\right)=C^1_4\cdot C^1_{18}=72\left(cách\right)\)
=>n(A)=1068
=>P=1068/1140=89/95