Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có phương trình tham số của d là:
d : x - 3 2 = y + 2 1 = z + 1 - 1
Suy ra tọa độ điểm M là nghiệm của phương trình:
3 + 2t - 2 + t - 1 - t + 2 = 0 nên t = -1 nên M ( 1;-2;0 )
Lại có VTPT của (P) là n P → 1 ; 1 ; 1 , VTCP của d là u d → 2 ; 1 ; - 1
Vì ∆ nằm trong (P) và vuông góc với d nên VTCP u ∆ → = u d → ; n p → = 2 ; 3 ; - 1
Gọi N ( x;y;z ) là hình chiếu vuông góc của M trên ∆ , khi đó M N → x - 1 ; y + 3 ; z
Ta có M N → vuông góc với u ∆ → nên ta có hệ phương trình: 2x - 3y + z - 11 = 0
Lại có N ∈ P và MN = 42 ta có hệ:
x + y + z = 2 2 x - 3 y + z - 11 = 0 x - 1 2 + y - 3 2 + z 2 = 42
Giải hệ ta tìm được hai nghiệm ( x;y;z ) là ( 5;-2;-5 ) và ( -3;-4;5 )
- Nếu N ( 5;-2;-5 ) ta có phương trình
∆ : x - 5 2 = y + 2 - 3 = z + 5 1
- Nếu N ( -3;-4;5 ) ta có phương trình
∆ = x + 3 2 = y + 4 - 3 = z - 5 1
Đáp án D

Chọn A
Tìm giao điểm I từ hệ phương trình đường thẳng d và mặt phẳng (P). Viết phương trình đường thẳng IM. Gọi tọa độ điểm M theo tham số của đường thẳng IM rồi xác định tham số đó từ phương trình I M = 4 14

Đáp án A
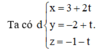
Vì M là giao điểm của d và (P) nên ta có tọa độ của M cũng thỏa mãn phương trình mặt phẳng (P) hay

Gọi điểm H là hình chiếu của M lên đường thẳng △ ta có
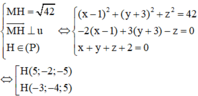
Vậy tồn tại hai đường thẳng △ thỏa mãn đề bài.
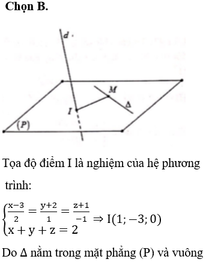


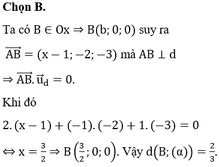


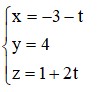
Đáp án B
Vì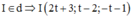 mà
mà 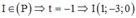
Vì M là hình chiếu vuông góc của I trên ∆
Khi đó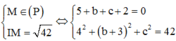
Vậy M(5; - 2; - 5) hoặc M(5; - 8;1) → bc=10