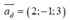Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

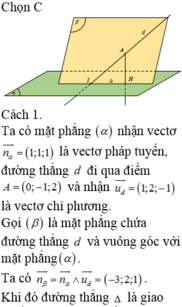
Chọn C
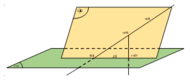
Ta có mặt phẳng α nhận vectơ n α → = ( 1 ; 1 ; 1 ) là vectơ pháp tuyến, đường thẳng d đi qua điểm A(0;-1;2) và nhận u d → = ( 1 ; 2 ; - 1 ) là vectơ chỉ phương.
Gọi β là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng α
![]()
Khi đó đường thẳng ∆ là giao tuyến của hai mặt phẳng α và β . Do đó một vectơ chỉ phương của đường thẳng ∆ là .
![]()
Mà u → = ( 1 ; a ; b ) nên a=4, b = -5 => a+b = 4-5 =-1.

Đáp án D
Đường thẳng d vuông góc với mặt phẳng (α) nên nhận véc-tơ ![]() làm véc-tơ chỉ phương.
làm véc-tơ chỉ phương.
Suy ra, phương trình đường thẳng d: 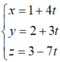 .
.

Chọn C
Gọi giao điểm của Δ và d là B nên ta có: B (3+t;3+3t;2t) ![]()
Vì đường thẳng Δ song song với mặt phẳng (α) nên:
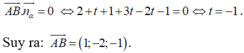
Phương trình đường thẳng Δ đi qua A và nhận 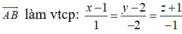

Đáp án C
![]()
có tâm I(4;3;3) bán kính R =4
Gọi phương trình đường thẳng d có dạng
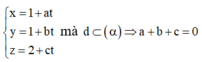
Khoảng cách từ tâm I đến d là
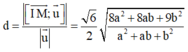
Ta có
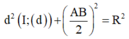
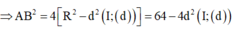
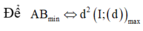
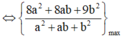
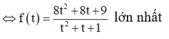
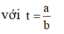
Khi đó

![]()

Đáp án A
Phương trình mặt phẳng (α): 2(x - 1) + 3(y + 2) + 5(z - 4)=0<=> 2x + 3y + 5z - 16=0.

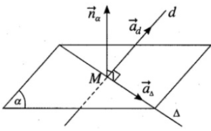
Xét phương trình:
2(1 + 2t) + (t) + (−2 – 3t) – 1 = 0 ⇔ 2t – 1= 0 ⇔ t = 1/2
Vậy đường thẳng d cắt mặt phẳng ( α ) tại điểm M(2; 1/2; −7/2).
Ta có vecto pháp tuyến của mặt phẳng ( α ) và vecto chỉ phương của đường thẳng d lần lượt là n α → = (2; 1; 1) và a d → = (2; 1; −3).
Gọi a ∆ → là vecto pháp tuyến của Δ, ta có a ∆ → ⊥ n α → và a ∆ → ⊥ a d →
Suy ra a ∆ → = n α → ∧ n d → = (−4; 8; 0) hay a ∆ → = (1; −2; 0)
Vậy phương trình tham số của
∆
là 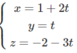
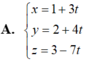

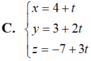
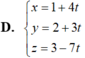

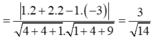


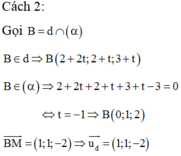


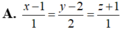
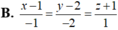

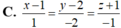
Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương