Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.Véc tơ nào trong các véc tơ sau đây không là véc tơ chỉ phương của đường thẳng d?
Đáp án D
Phương pháp:
Đường thẳng d: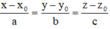 
có 1 VTCP là 
. Mọi vectơ
v
→
=
k
u
→
(
k
∈
Z
)
cùng phương với vecto
u
→
đều là VTCP của đường thẳng d
Cách giải: Đường thẳng d nhận u 1 → = 1 ; - 1 ; 1 là 1 VTCP. Mọi vecto cùng phương với vecto đều u → là VTCP của đường thẳng d.
Ta thấy chỉ có đáp án D, vecto u 1 → = 1 ; 1 ; 1 không cùng phương với u 1 → = 1 ; - 1 ; 1 nên u 1 → = 1 ; 1 ; 1 không là VTCP của đường thẳng d
Đáp án D
Điểm A ( 2 ; 1 ; − 3 ) , B ( 2 ; 4 ; 1 ) , O 0 ; 0 ; 0 suy ra G là trọng tâm tam giác ABO là G 2 3 ; 5 3 ; − 2 3
Gọi M, N, P lần lượt là hình chiếu vuống góc cuả A, B, O trên đường thẳng d
Khi đó, khoảng cách:
d A → d = A M ; d B → d = B N ; d O → d = O P
Mặt khác A M ≤ A G B N ≤ B G O P ≤ O G
⇒ d A → d + d B → d + d O → d ≤ A G + B G + O G = c o n s t
Dấu “=” xảy ra khi và chỉ khi đường thẳng d vuông góc mặt phẳng A B O tại G
Ta có O A → = 2 ; 1 ; − 3 O B → = 2 ; 4 ; 1 ⇒ n A B O → = 13 ; − 8 ; 6
⇒ véc tơ chỉ phương của (d) là u → = − 13 ; 8 ; − 6
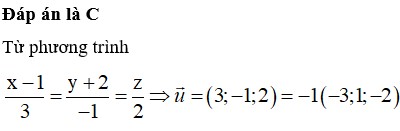
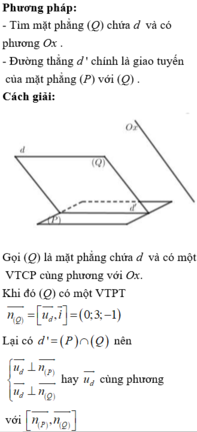
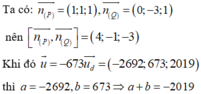
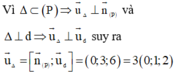
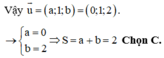
Đáp án là C