Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B

Đáp án B.
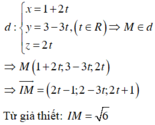
⇔ 2 t − 1 2 + 2 − 3 t 2 + 2 t + 1 2 = 6 ⇔ 4 t 2 − 4 t + 1 + 4 − 12 t + 9 t 2 + 4 t 2 + 4 t + 1 = 6
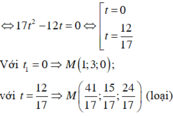


- Tính khoảng cách từ B đến d theo t và tìm GTLN của khoảng cách.
- Tìm t và suy ra tọa độ của M.
Cách giải:
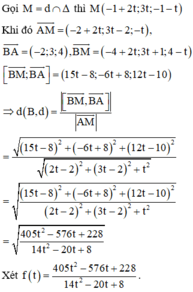
Sử dụng MTCT (chức năng TABLE với bước START nhập -5, bước END nhập 5 và bước STEP nhập 1 ta sẽ được kết quả GTLN f t = 29 tại t = 2)


Đáp án A
Ta có A B → = 2 ; 1 ; 2 A C → = - 2 ; 2 ; 1 ⇒ A B → ; A C → = - 3 ; - 6 ; 6 ⇒ S ∆ A B C = 1 2 A B → , A C → = 9 2
Phương trình mặt phẳng (ABC) là - 3 x - 0 - 6 y - 1 + 6 z - 0 = 0 ⇔ x + 2 y - 2 z - 2 = 0
Điểm M ∈ d ⇒ M 2 t + 1 ; - t - 2 ; 2 t + 3 ⇒ d M , A B C = 4 t + 11 3 1
Lại có V M . A B C = 1 3 d M , A B C . S ∆ A B C ⇒ d M , A B C = 2 2
Từ (1) và (2) suy ra 4 t + 11 3 = 2 ⇔ 4 t + 11 = 6 ⇔ [ t = - 5 4 t = - 17 4 . Vậy [ M 1 - 15 2 ; 9 4 ; - 11 2 M 2 - 3 2 ; - 3 4 ; 1 2 .

Đáp án D.
Ta có
A B → = − 4 ; 2 ; 4 , A C → = 2 ; − 1 ; − 2 ⇒ A , B , C
thẳng hàng nên không có D thỏa mãn.
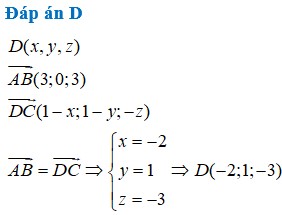


Đáp án D
Vì ABCD là hình thang ⇒ A D / / B C ⇒ u → A D = u → B C = − 5 ; − 2 ; 1
=>Phương trình đường thẳng AD là x + 2 − 5 = y − 3 − 2 = z − 1 1 ⇒ D − 5 t − 2 ; − 2 t + 3 ; t + 1
Ta có S A B C D = 3 S Δ A B C ⇔ S Δ A B C + S Δ A C D = 3 S Δ A B C ⇔ S Δ A C D = 2 S Δ A B C
Mà diện tích tam giác ABC là S Δ A B C = 1 2 A B ¯ ; A C ¯ = 341 2 ⇒ S Δ A C D = 341
Mặt khác A D ¯ ; A C ¯ = 341 t 2 ⇒ 1 2 341 t 2 = 341 ⇔ t = 2 t = − 2 ⇒ D − 12 ; − 1 ; 3 D 8 ; 7 ; − 1
Vì ABCD là hình thang → D − 12 ; − 1 ; 3