Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(\overrightarrow{AB}=\left(-a;b;0\right)\)
và \(\overrightarrow{AC}=\left(-a;0;c\right)\)
Vì \(\overrightarrow{AB}.\overrightarrow{AC}=a^2>0\) nên góc \(\widehat{BAC}\) là góc nhọn
Lập luận tương tự chứng minh được các góc \(\widehat{B}\) và \(\widehat{C}\) cũng là góc nhọn

Chọn A.

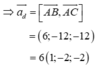
Đường thẳng d đi qua G(2;-1;0) và có vectơ chỉ phương là ![]()
Vậy phương trình tham số của d là 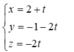

Chọn C
Do tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc và H là trực tâm tam giác ABC nên ![]()
Phương trình mặt phẳng (ABC) là ![]() hay 6x + 4y + 3z - 12 = 0
hay 6x + 4y + 3z - 12 = 0
Vì ![]() nên đường thẳng OH có véc-tơ chỉ phương
nên đường thẳng OH có véc-tơ chỉ phương ![]()
Mà đường thẳng OH đi qua O nên phương trình tham số của đường thẳng OH là: 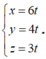


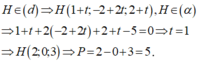



Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.