Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi pt mặt phẳng cần tìm là: x a + y b + z c = 1 M ( 1 ; 1 ; 2 ) ∈ ( P ) ⇒ 1 a + 1 b + 2 c = 1 ( * ) A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) : O A = O B = O C ⇒ a = b = c = α > 0 ⇒ ( a ; b ; c ) ∈ { ( α ; α ; α ) , ( − α ; α ; α ) , ( α ; − α ; α ) , ( α ; α ; − α ) , ( − α ; − α ; α ) , ( − α ; α ; − α ) , ( α ; − α ; − α ) , ( − α ; − α ; − α ) }
Thay vào (*) ta thấy chỉ có 3 bộ thỏa mãn: ( α ; α ; α ) , ( − α ; α ; α ) , ( α ; − α ; α ) tương ứng có 3 mặt phẳng thỏa mãn đề bài

Đáp án B
Vì OA, OB, OC đôi một vuông góc và M là trực tâm Δ A B C ⇒ O M ⊥ A B C
Suy ra mp A B C nhận O M → làm véc tơ pháp tuyến và đi qua điểm M(1;2;3)
Vậy phương trình m p P : 1. x − 1 + 2. y − 2 + 3. z − 3 = 0 ⇔ x + 2 y + 3 z − 14 = 0

Đáp án D
Kiến thức: Chóp tam giác có 3 cạnh bên đôi một vuông góc với nhau thì hình chiếu của đỉnh trên mặt đáy trùng với trực tâm của đáy.
Chóp O.ABC có các cạnh OA, OB, OC đôi một vuông góc với nhau, M(2;1;5) là trực tâm ΔABC .
⇒ O M ⊥ A B C ≡ P , vậy (P) nhận O M → = ( 2 ; 1 ; 5 ) làm một vectơ pháp tuyến. → Phương trình mặt phẳng (P) là:
2 x − 2 + y − 1 + 5 z − 5 = 0 ⇔ 2 x + y + 5 z − 30 = 0
Vậy d I ; P = 2 + 2 + 15 − 30 4 + 1 + 25 = 11 30 30

Đáp án B
 Gọi
A
=
∆
∩
P
;
d
=
P
∩
Q
Gọi
A
=
∆
∩
P
;
d
=
P
∩
Q
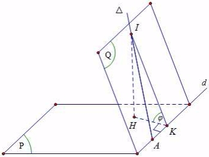
Lấy I ∈ ∆ ⇒ A ; I cố định, kẻ I H ⊥ P ; H K ⊥ d ⇒ P ; Q ^ = I K H ^ = φ
Do I A ≥ I K ⇒ sin φ = I H I K ≥ I H I A ⇒ φ m i n khi K ≡ A tức là I A ⊥ d ⇒ n Q → = u ∆ → ; u d →
Trong đó n ∆ ¯ = 1 ; - 2 ; - 2 ; u d ¯ = u ∆ ¯ ; u P ¯ = 3 ; 0 ; 3 = 3 1 ; 0 ; 1
Suy ra n Q ¯ = u ∆ ¯ ; u d ¯ = - 2 1 ; 1 ; - 1 , mặt khác (Q) chứa đường thẳng ∆ nên (Q) đi qua điểm (1;2;-1)
Do đó Q : x + y - z - 4 = 0 ⇒ A 4 ; 0 ; 0 , B ( 0 ; 4 ; 0 ) , C ( 0 ; 0 ; - 4 ) ⇒ V O . A B C = 64 6 = 32 3

Đáp án C.
Đặt A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c .
Mà M là trọng tâm tam giác ABC ⇒ a 3 = 1 b 3 = 2 c 3 = 3 ⇔ a = 3 ; b = 6 ; c = 9 .
Phương trình mặt phẳng P : x 3 + y 6 + z 9 = 1 ⇔ 6 x + 3 y + 2 z − 18 = 0 .

Đáp án C.
Đặt A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c .
Mà M là trọng tâm tam giác ABC ⇒ a 3 = 1 b 3 = 2 c 3 = 3 ⇔ a = 3 ; b = 6 ; c = 9 .
Phương trình mặt phẳng P : x 3 + y 6 + z 9 = 1 ⇔ 6 x + 3 y + 2 z - 18 = 0 .


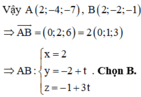

Chọn C