Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Sử dụng công thức viết phương trình mặt phẳng dạng đoạn chắn: Mặt phẳng (ABC) đi qua các điểm A(a;0;0), B(0;b;0), C(0;0;c) có phương trình
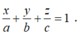
Cách giải: Phương trình mặt phẳng (ABC): x 2 + y 3 + z 4 = 1

Đáp án D
Áp dụng công thức phương trình mặt phẳng theo đoạn chắn ta được (ABC):
![]()

Phương trình mp theo đoạn chắn:
\(\dfrac{x}{1}+\dfrac{y}{3}+\dfrac{z}{5}=1\)
\(\Leftrightarrow15x+5y+3z-15=0\)

Đáp án B
Phương pháp: - Trọng tâm G của tam giác ABC có tọa độ được tính:
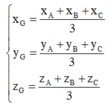
- Phương trình mặt phẳng đi qua M x 0 ; y 0 ; z 0 và có 1 VTPT n → =(a;b;c)
![]()
Cách giải: Trọng tâm G của tam giác ABC: G(-1;1;1)
(P) vuông góc với AB => (P) nhận A B → = ( 2 ; 2 ; - 3 ) là một VTPT
Phương trình mặt phẳng (P):
![]()
![]()

\(\overrightarrow{AB}=\left(2;3;2\right)\Rightarrow AB=\sqrt{2^2+3^2+2^2}=\sqrt{17}\)
\(\overrightarrow{BC}=\left(-3;0;-1\right)\Rightarrow BC=\sqrt{\left(-3\right)^2+0^2+\left(-1\right)^2}=\sqrt{10}\)
\(\left[\overrightarrow{AB};\overrightarrow{BC}\right]=\left(-3;-4;9\right)\)
Mặt phẳng (ABC) nhận (-3;-4;9) là 1 vtpt
Phương trình (ABC):
\(-3\left(x-1\right)-4\left(y+2\right)+9\left(z-4\right)=0\)
\(\Leftrightarrow-3x-4y+9z-41=0\)
\(d\left(M;\left(ABC\right)\right)=\dfrac{\left|-3.2+4.1+9.3-41\right|}{\sqrt{\left(-3\right)^2+\left(-4\right)^2+9^2}}=\dfrac{8\sqrt{106}}{53}\)


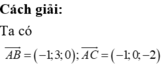



\(\overrightarrow{BA}=\left(3;-2;2\right)\) ; \(\overrightarrow{CA}=\left(2;-1;3\right)\)
\(\Rightarrow\left[\overrightarrow{CA};\overrightarrow{BA}\right]=\left(4;5;-1\right)\)
\(\Rightarrow\left(ABC\right)\) nhận \(\left(4;5;-1\right)\) là 1 vtpt
Phương trình mp (ABC):
\(4\left(x-0\right)+5\left(y-3\right)-1\left(z-0\right)=0\)
\(\Leftrightarrow4x+5y-z-15=0\)