Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

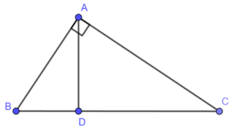
Xét hai tam giác vuông DAC và DBA ,ta có:
∠ (ADC) = ∠ (BDA) = 90 0
∠ C = ∠ (DAB) (hai góc cùng phụ ∠ B )
Suy ra: △ DAC đồng dạng △ DBA (g.g)
Suy ra: 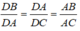
⇒ D A 2 = D B . D C
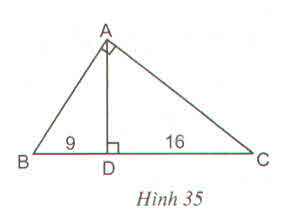
hay DA = D B . D C = 9 . 16 = 12 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
A B 2 = D A 2 + D B 2 = 9 2 + 12 2 = 225 ⇒ AB =15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:
AC2 = DA2 + DC2 = 122 +162 = 400 ⇒ AC = 20cm
Vậy BC = BD + DC = 9 + 16 = 25(cm)

Tam giác ABC vuông tại A với đường cao AH và trung tuyến AM
Theo tính chất trung tuyến ứng với cạnh huyền, ta có \(AM=\dfrac{BC}{2}\)
\(\dfrac{AH}{AM}=\dfrac{40}{41}\Leftrightarrow\dfrac{AH}{\dfrac{BC}{2}}=\dfrac{40}{41}\Leftrightarrow AH=\dfrac{20}{41}BC\) (1)
Xét hai tam giác vuông ABH và CBA có \(\widehat{B}\) chung
\(\Rightarrow\Delta ABH\sim\Delta CBA\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{BC}\Leftrightarrow AB.AC=AH.BC\) (2)
Thay (1) vào (2): \(AB.AC=\dfrac{20}{41}BC^2\Leftrightarrow\dfrac{41}{20}AB.AC=BC^2\)
Theo định lý Pitago: \(AB^2+AC^2=BC^2\Rightarrow AB^2+AC^2=\dfrac{41}{20}AB.AC\) (3)
Do các cạnh tam giác đều lớn hơn 0, chia 2 vế của (3) cho \(AB.AC\):
\(\dfrac{AB}{AC}+\dfrac{AC}{AB}=\dfrac{41}{20}\Rightarrow\) đặt \(\dfrac{AB}{AC}=x>0\) ta được:
\(x+\dfrac{1}{x}=\dfrac{41}{20}\Leftrightarrow x^2-\dfrac{41}{20}x+1=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{4}{5}\end{matrix}\right.\)
Vậy tỉ số giữa 2 cạnh góc vuông là \(\dfrac{4}{5}\) ( hoặc \(\dfrac{5}{4}\))

\(AB^2 + AC^2 = 25^2 = 625\)
\(AD^2 + 81 = AB^2\)
\(AD^2 + 256 = AC^2\)
\(=> AD^2 + 81 + AD^2 + 256 = 625\)
=> \(2AD^2 = 288\)
=> \(AD^2 = 144\)
=> AD = 12(cm)
=>\( AB^2 = 9^2 + 12^2 = 225\)
=> AB = 15 (cm)
=> \(AC^2 = 12^2 + 16^2 = 400\)
=> AC = 20(cm)
và BC = 25(cm)

Ta có: \(BC=BD+DC=9+16=25\left(cm\right)\)
Xét \(\Delta DBA\) và \(\Delta ABC\):
\(\widehat{A}=\widehat{D}\left(=90^o\right)\)
\(\widehat{B}=\widehat{A_2}\)(cùng phụ với góc\(A_1\))
\(\Rightarrow\Delta DBA\)~\(\Delta ABC\)
\(\Rightarrow\dfrac{DB}{AB}=\dfrac{AB}{BC}\Leftrightarrow AB^2=DB.BC=9.25=225\Rightarrow AB=15\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC, có:
\(AB^2+AC^2=BC^2\Leftrightarrow15^2+AC^2=25^2\Rightarrow AC=\sqrt{25^2-15^2}=20\)
Vậy các cạnh của tam giác vuông ABC lần lượt là: \(15;20;25\)

Làm ơn cho tớ hỏi đường cao có phải là đường cao ứng với cạnh huyền không?