Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Số nghiệm của phương trình f(x) = m + 1 bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m + 1
Cách giải:
Phương trình f(x) = m + 1 vô nghiệm ⇔ -2 ≤ m + 1 < 1 ⇔ -3 ≤ m < 0

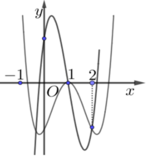
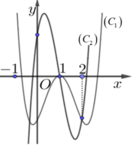
+ Ta có y = f ( x ) = f ( x ) , f ( x ) ≥ 0 - f ( x ) , f ( x ) < 0 . Từ đó suy ra cách vẽ đồ thị hàm số (C) như sau:
- Giữ nguyên đồ thị y= f (x) phía trên trục hoành.
- Lấy đối xứng phần đồ thị y= f(x) phía dưới trục hoành qua trục hoành ( bỏ phần dưới ).
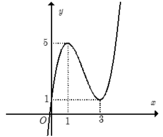
Kết hợp hai phần ta được đồ thị hàm số y = f ( x ) như hình vẽ.
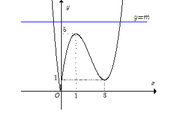
Phương trình f ( x ) = m là phương trình hoành độ giao điểm của đồ thị hàm số y = f ( x ) và đường thẳng
y= m (cùng phương với trục hoành).
Dựa vào đồ thị, ta có ycbt
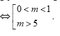
Chọn D.

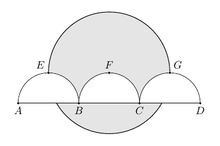
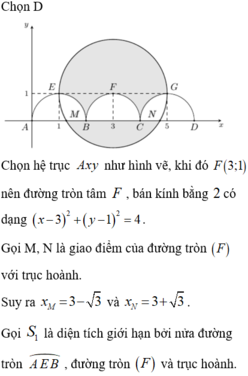
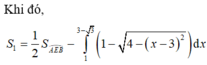
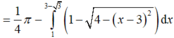
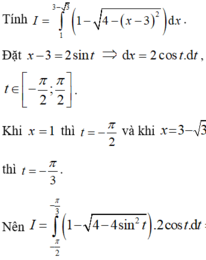

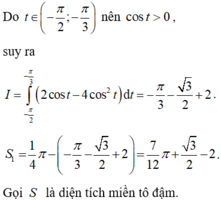
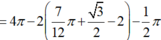
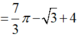
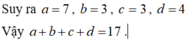



ai giúp đi
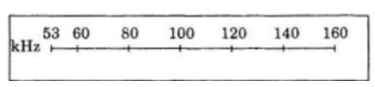
a) Theo giả thiết ta có: d = 0 => F = 53 <=> k.a0=53 <=> k = 53
Và d = 12 => F = 160 <=> k.a12=160
c) Từ câu b) => d = 25,119.lgF-43,312
(do yêu cầu kết quả tính chính xác đến hàng phần trăm)
Vậy ta có bảng.