Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(v_1\) là vận tốc của xe xuất phát từ A, \(v_2\) là vận tốc của xe xuất phát từ B, \(t_1\) là khoảng thời gian từ lúc xuất phát đến lúc gặp nhau lần 1, \(t_2\) là khoảng thời gian từ lúc gặp nhau lần 1đến lúc gặp nhau lần 2 và đặt x = AB.
Gặp nhau lần 1: \(v_1t_1=30,v_2t_1=x-30\) suy ra \(\frac{v_1}{v_2}=\frac{30}{x-30}\)
Gặp nhau lần 2: \(v_1t_2=\left(x-30\right)+36=x+6;\)\(v_2t_2=30+\left(x-36\right)=x-6\)
suy ra \(\frac{v_1}{v_2}=\frac{x+6}{x-6}\)
Từ (1) và (2) suy ra x = 54km.
Thay x = 54 km vào (1) ta được \(\frac{v_1}{v_2}=1,25\) hay \(\frac{v_2}{v_1}=0,8\)

gọi v1 là vận tốc của xe thứ nhất
v2 là vận tốc và của xe thứ hai
s1 là khoảng cách của 2 xe đi ngược chiều trong thời gian t
s2 là khoảng cách của 2 xe đi cùng chiều trong thời gian t
t là thời gian cả 2 xe đi
t=10s
Ta có
s1=t(v1+v2)=>10(v1+v2)=> v1+v2=1,5(m)(1)
s2=t(v1-v2)=>10(v1-v2)=> v1-v2=0,4(m)(2)
từ (1)và(2)=>v1+v2=1,5
v1-v2=0,4
v1=0,95(m/s)
v2=0,55(m/s)
quãng đường vật 1 đi đc trong 30s là
s1=v1.t'=0.95.30=28,5(m)
s2=v2.t=0.55.30=16,5(m)

Đáp án D
Ta để ý rằng tại mỗi thời điểm v luôn vuông pha với x, từ phương trình
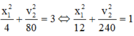
→ v 2 vuông pha với x 1 → hai dao động hoặc cùng pha hoặc ngược pha nhau
Ta có:
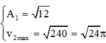
Với hai dao động cùng pha thì thời gian để hai dao động gặp nhau là
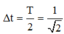
![]()
![]()
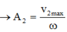
![]() luôn cùng li độ → loại
luôn cùng li độ → loại
Với hai dao động ngược pha thì thời gian để hai dao động gặp nhau là
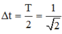
![]()
![]()
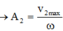
![]()
![]()

đề bị sai rồi xuất phát cùng lúc mà cùng vận tốc , => gặp nhau giữa AB
=> s= nhau
ta có s , t cùng lúc,v (= nhau )
mà thời gian đi khác nhau là sao ?
Bởi vì nước chảy nên cano này xuôi dòng thì cano kia ngược dòng và ngược lại
do vậy nên vận tốc bị thay đổi dẫn đến chênh lệch thời gian