

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)

Chọn D.
Đặt t = 2x + 2-x, suy ra t2 = 22x + 2 -2x + 2.
Ta có ![]()
Phương trình trở thành
![]()
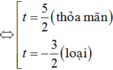
![]()
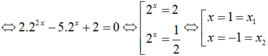
khi đó ; S = x1+ x2 = 0.

Ta xét các trường hợp sau:
+ TH1. x- 3= 1 hay x= 4. Khi đó; phương trình đã cho trở thành : 112= 1 luôn đúng.
=> x= 4 là nghiệm của phương trình.
+ TH2. .
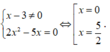
Vậy phương trình đã cho có ba nghiệm
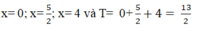
Chọn C.

\(log_2x\left(log_3x-1\right)+x\left(log_3x-1\right)-3\left(log_3x-1\right)=0\)
\(\Leftrightarrow\left(log_3x-1\right)\left(log_2x+x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\log_2x+x-3=0\end{matrix}\right.\)
Xét hàm \(f\left(x\right)=log_2x+x-3\) có \(f'\left(x\right)=\dfrac{1}{xln2}+1>0;\forall x>0\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)\) có tối đa 1 nghiệm
Nhận thấy \(x=2\) là nghiệm nên x=2 là nghiệm duy nhất
Tổng =2+3