K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 12 2020
\(S=\dfrac{1}{2018!\left(2019-2018\right)!}+\dfrac{1}{2016!\left(2019-2016\right)!}+...+\dfrac{1}{2!\left(2019-2\right)!}+\dfrac{1}{0!\left(2019-0!\right)}\)
\(\Rightarrow2019!.S=\dfrac{2019!}{2018!\left(2019-2018\right)!}+\dfrac{2019!}{2016!\left(2019-2016\right)!}+...+\dfrac{2019!}{2!\left(2019-2\right)!}+\dfrac{2019!}{0!\left(2019-0\right)!}\)
\(=C_{2019}^{2018}+C_{2019}^{2016}+...+C_{2019}^2+C_{2019}^0\)
\(=\dfrac{1}{2}\left(C_{2019}^0+C_{2019}^1+...+C_{2019}^{2018}+C_{2019}^{2019}\right)\)
\(=\dfrac{1}{2}.2^{2019}=2^{2018}\)
\(\Rightarrow S=\dfrac{2^{2018}}{2019!}\)
CM
2 tháng 6 2018
Đáp án C
Số các số gồm 5 chữ số đôi 1 khác nhau là: 5! = 120 số
Trong mỗi hàng do các số có khả năng xuất hiện như nhau nên mỗi số xuất hiện 120:5=24 lần
⇒ S= 9333240
CM
21 tháng 8 2018
Đáp án C
Số phần tử của tập S là 5! = 120 số.
Mỗi số 5, 6, 7, 8, 9 có vai trò như nhau và xuất hiện ở hàng đơn vị 4! = 24 lần
Tổng các chữ số xuất hiện ở hàng đơn vị là 4!.(5 + 6 + 7 + 8 + 9) = 840
Tương tự với các chữ số hàng chục, hàng tram, hàng nghìn và hàng chục nghìn.
Vậy tổng tất cả các số thuộc tập S là 840.(104+103+102+10+1) = 9333240
12 tháng 5 2023
n(S)=6!
Để thỏa mãn yêu cầu đề bài thì cần chọn ra 3 số có tổng là 12
=>Số trường hợp thỏa mãn là (1;5;6); (2;4;6); (3;4;5)
=>Có 3*3!*3!
=>P=3/20
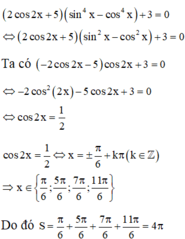
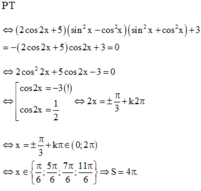
Giải ko cần sử dụng nhị thức Newton:
\(S=5+2.5^2+3.5^3+...+49.5^{49}+50.5^{50}\)
\(\Rightarrow5S=5^2+2.5^3+3.5^4+...+49.5^{50}+50.5^{51}\)
Trừ dưới cho trên:
\(4S=-5-5^2-5^3-5^4-...-5^{50}+50.5^{51}\)
\(\Rightarrow4S=5.5^{51}-\left(5+5^2+...+5^{50}\right)\)
Chú ý rằng trong ngoặc là tổng cấp số nhân với \(\left\{{}\begin{matrix}u_1=5\\q=5\end{matrix}\right.\)
\(\Rightarrow4S=5.5^{51}-\frac{5^{51}-5}{4}=\frac{19}{4}.5^{51}+\frac{5}{4}\)
\(\Rightarrow S=\frac{19.5^{51}+5}{16}\)
E cảm ơn ạ !