Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
x = 7
=> x + 1 = 8 (1)
Thay (1) vào biểu thức ta được
\(x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}-\left(x+1\right)x^{12}+...-\left(x+1\right)x^2+\left(x+1\right)x-5\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}-x^{13}-x^{12}+...-x^3-x^2+x^2+x-5\)
\(=x-5\)
\(=7-5\)
\(=2\)
Ta có :
= x^15 - 8x^14 + 8x^13 - 8x^12 +... - 8x² + 8x - 5= x^15 - 8x^13(x - 1) - 8x^11(x-1) +... - 8x(x - 1) - 5
= x^15 - 8(x - 1)(x^13 + x^11 +... + x) - 5 (♠)
Xét : A = x^13 + x^11 + x^9 + x^7+... + x³ + x
⇔ x².A = x^15 + x^13 + x^11 + x^9 + x^7 +... + x³
⇔x².A - A = (x^15 + x^13 + x^11 + x^9 +... + x³) - (x^13 + x^11 + x^9 + x^7+... + x) = x^15 - x
⇔ A = (x^15 - x)/(x² - 1)
Thay vào (♠) ta được :
P = x^15 - 8(x - 1)(x^15 - x)/(x² - 1) - 5
= x^15 - 8(x^15 - x)/(x + 1) - 5
Thay x = 7 vào biểu thức trên ta được : P = 7^15 - 8(7^15 - 7)/(7+1) - 5 = 2
Vậy giá trị của biểu thức bằng 2
Đáp án là A.
Ta có:
x = log 2 3 ; y = log 3 4 ⇒ P = 8 log 2 3 + 9 log 3 4 = 3 3 + 4 2 = 43.
Chọn đáp án B
Từ giả thiết ta có:
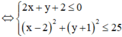
Suy ra tập hợp các điểm biểu diễn số phức z là miền mặt phẳng
(T) thỏa mãn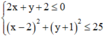 
(miền tô đậm trong hình vẽ bên
Gọi A, B là các giao điểm của đường thẳng 2 x + y + 2 = 0 và đường tròn (C’) : x - 2 2 + y + 1 2 = 25
Ta tìm được A(2; -6) và B(-2; 2)
Ta có :
Đường tròn (C) cắt miền (T) khi và chỉ khi
Chọn đáp án B
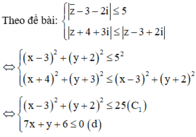
=> Tập hợp các điểm biểu diễn số phức z là miền mặt phẳng (T) mà tọa độ các điểm thỏa mãn hệ (*)
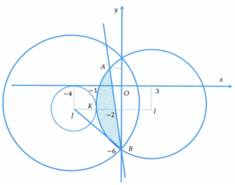
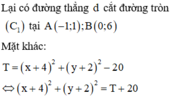
Đáp án D
Ta có C 12 1 . C 10 1 = 120
Khi đó C 12 1 . C 10 1 = 120 . Đặt C 12 1 . C 10 1 = 120
Ta luôn có C 12 1 . C 10 1 = 120
C 12 1 . C 10 1 = 120 Suy ra C 12 1 . C 10 1 = 120
Xét hàm số f t = t 2 − 8 t + 3 trên khoảng − 1 ; + ∞ ,có f ' t = 2 t + 1 2 t + 4 t + 3 2 > 0 ; ∀ t > − 1
Hàm số f(t) liên tục trên − 1 ; + ∞ ⇒ f t đồng biến trên − 1 ; + ∞
Do đó, giá trị nhỏ nhất của f(t) là min − 1 ; + ∞ f t = f − 1 = − 3 . Vậy P min = − 3
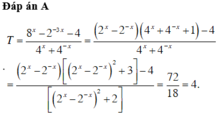
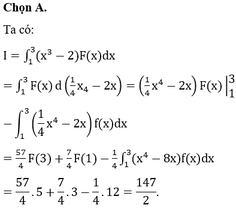
\(x^{15}-\left(7+1\right)x^{14}+\left(7+1\right)x^{13}....+\left(7+1\right)x-5\)
\(=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}....+\left(x+1\right)x-5\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}....-x^3-x^2+x^2+x-5\)
\(=x-5=7-5=2\)
ai ma biet