Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có ABCD là hình bình hành nên A D ⇀ = B C ⇀ = - 1 ; 3 ; 7 ⇒ D 0 ; 5 ; 10
Chọn đáp án C.

Đáp án A
Ta có 5 log c 6 = 6 log c 5 ⇔ 5 log c 6 + − 6 log c 5 = 0 . Mà
f − x = a ln 2017 x 2 + 1 − x − b x sin 2018 x + 2
a ln 2017 1 x 2 + 1 + x − b x sin 2018 x + 2 = − a ln 2017 x 2 + 1 + x − b x sin 2018 x + 2
⇒ f x + f − x = 4 ⇒ f − 6 log c 5 + f 5 log c 6 = 4 ⇒ f − 6 log c 5 = − 2

Ta có P = log a 2 b + 16 log b a
Đặt t = log a b
Xét hàm số
f t = t 2 + 16 t f ' t = 2 t - 16 t 2 = 0 ⇔ t = 2
Với t = 2 ta có log a b = 2 ⇒ a 2 = b . Thay b = a 2 vào k ta được k = log a a b 3 = log a a . a 2 3 = 1
Đáp án A

Đáp án A
Ta có 5 log c 6 = 6 log c 5 = x ⇒ − 6 log c 5 = − x
Khi đó f − x = a . ln 2017 x 2 + 1 − x − b x sin 2018 x + 2
= a . ln 2017 1 x 2 + 1 + x − b x sin 2018 x + 2
= − a . ln 2017 x 2 + 1 + b x sin 2018 x + 2 + 4
Mặt khác f x = 6 → P = f − x = − f x + 4 = − 6 + 4 = − 2

Lời giải:
Bài 1)
Nếu \(p^2-1\in\mathbb{P}\Rightarrow (p-1)(p+1)\in\mathbb{P}\)
Khi đó trong hai thừa số $p-1$ hoặc $p+1$ phải có một thừa số có giá trị bằng $1$, số còn lại là số nguyên tố. Vì $p-1<p+1$ nên \(p-1=1\Rightarrow p=2 \in\mathbb{P} \Rightarrow p+1=3\in\mathbb{P}(\text{thỏa mãn})\)
Khi đó \(8p^2+1=33\) là hợp số. Do đó ta có đpcm.
P/s: Hẳn là bạn chép nhầm đề bài khi thêm dữ kiện $p>3$. Với $p>3$ thì $p^2-1$ luôn là hợp số bạn nhé.
Câu 2:
a) Câu này hoàn toàn dựa vào tính chất của số chính phương
Ta biết rằng số chính phương khi chia $3$ có dư là $0$ hoặc $1$. Mà \(p,q\in\mathbb{P}>3\Rightarrow \) $p,q$ không chia hết cho $3$. Do đó:
\(\left\{\begin{matrix} p^2\equiv 1\pmod 3\\ q^2\equiv 1\pmod 3\end{matrix}\right.\Rightarrow p^2-q^2\equiv 0\pmod 3\Leftrightarrow p^2-q^2\vdots3(1)\)
Mặt khác, vì số chính phương lẻ chia cho $8$ luôn có dư là $1$ nên
\(p^2\equiv 1\equiv q^2\pmod 8\Rightarrow p^2-q^2\equiv 0\pmod 8\Leftrightarrow p^2-q^2\vdots 8\)$(2)$
Từ $(1)$, $(2)$ kết hợp với $(3,8)=1$ suy ra \(p^2-q^2\vdots 24\)
b) Vì \(a,a+k\in\mathbb{P}>3\) nên $a,a+k$ phải lẻ. Do đó $k$ phải chẵn \(\Rightarrow k\vdots 2\) $(1)$
Mặt khác, từ điều kiện đề bài suy ra $a$ không chia hết cho $3$. Do đó $a$ chia $3$ dư $1$ hoặc $2$. Nếu $k$ cũng chia $3$ dư $1$ hoặc $2$ ( $k$ không chia hết cho $3$) thì luôn tồn tại một trong hai số $a+k$ hoặc $a+2k$ chia hết cho $3$ - vô lý vì $a+k,a+2k\in\mathbb{P}>3$
Do đó $k\vdots 3$ $(2)$
Từ $(1)$ và $(2)$ kết hợp $(2,3)=1$ suy ra $k\vdots 6$ (đpcm)

Ta có
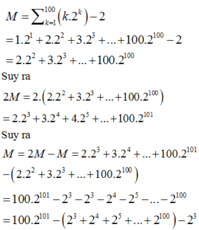
Xét tổng 2 3 + 2 4 + . . + 2 100 là tổng của 98 số hạng của cấp số nhân có u 1 = 2 3 và công bội q = 2 .
Nên
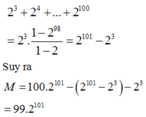
Từ đó
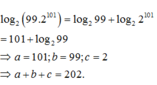
Chọn B.

Ta có ABCD là hình bình hành
⇔ C D → = B A → ⇔ d - c = a - b ⇔ d = a + c - b ⇔ d = 8 + m - 3 i
ABCD là hình chữ nhật
⇔ A V = B D ⇔ c - a = d - b ⇔ 3 + m + 2 i = 9 + m - 4 i ⇔ 3 2 + m + 2 2 = 9 2 + m - 4 2 ⇔ m = 7
Đáp án C

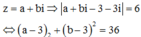
Đặt x = a - 1 6 ; y = b - 1 6 . Khi đó
K = x + y x 2 - x y + y 2 x 3 - y 3 = x 3 + y 3 x 3 - y 3 = x 6 - y 6 = a - 1 - b = 1 - a b a
Đáp án D