K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
AH
Akai Haruma
Giáo viên
23 tháng 2 2021
Lời giải:
Trước tiên ta tìm giao điểm của 2 ĐTHS:
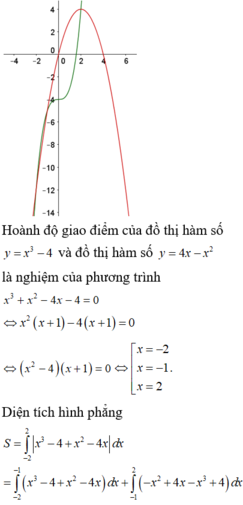
PT hoành độ giao điểm: $|x^2-4x+3|=x+3$
$\Rightarrow x=0$ hoặc $x=5$
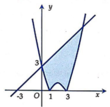
Diện tích hình phẳng giới hạn bởi $(C)$ và $(d)$ là:
\(\int ^5_0(x+3-|x^2-4x+3|)dx=\frac{109}{6}\) (đơn vị diện tích)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
Phương trình hoành độ giao điểm:
\(2x^3-3x^2+1=x^3-4x^2+2x+1\)
\(\Leftrightarrow x^3+x^2-2x=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=0\\x=1\end{matrix}\right.\)
Trên \(\left(-2;0\right)\) ta có \(x^3+x^2-2x>0\) và trên \(\left(0;1\right)\) ta có \(x^3+x^2-2x< 0\)
Do đó:
\(S=\int\limits^0_{-2}\left(x^3+x^2-2x\right)dx-\int\limits^1_0\left(x^3+x^2-2x\right)dx=\dfrac{8}{3}+\dfrac{5}{12}=\dfrac{37}{12}\)
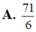
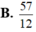
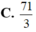
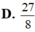
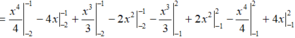
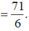
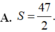
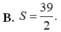
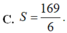
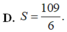
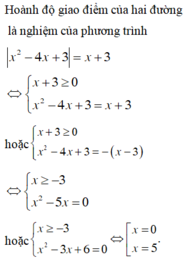
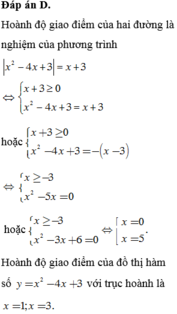
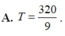
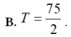
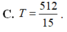
Chọn B.
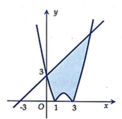
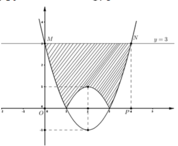
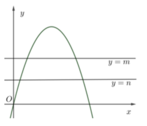
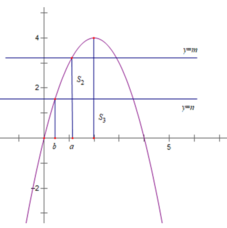
Ta thấy đường thẳng y = -4x - 4 và đường thẳng y = 4x - 4 lần lượt là hai tiếp tuyến của đồ thị hàm số y = x2 tại các tiếp điểm có hoành độ x = -2 và x = 2.
Do tính đối xứng qua Oy của parabol y = x2 nên diện tích hình phẳng cần tìm bằng 2 lần diện tích tam giác cạnh OMT2 và bằng:
S = 2 ∫ 0 2 x 2 - 4 x - 4 d x = 2 ∫ 0 2 x - 2 2 d x = 2 ( x - 2 ) 3 3 2 0 = 16 3