Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi S là diện tích hình phẳng cần tìm. Đó f x > 0 , ∀ x ∈ 1 ; e 2 nên
S = ∫ 1 e 2 f x d x = ∫ 1 e 2 x + 1 ln x d x
Đặt
u = ln x d v = x + 1 d x ⇒ d u = 1 x d x v = 2 3 x x + x
Khi đó
S = 2 x 3 + 1 x ln x 1 e 2 - ∫ 1 e 2 2 x 3 + 1 d x = 8 e 3 + 8 e 2 + 13 9
Đáp án D

Gọi S là diện tích hình phẳng cần tìm. Do f(x) > 0 ∀ x ∈ 1 ; e 2
nên S = ∫ 1 e 2 f x d x = ∫ 1 e 2 x + 1 x d x
Đặt u = ln x d v = x + 1 d x ⇒ d u = 1 x d x v = 2 3 x x + x
Khi đó
S = 2 x 3 + 1 x ln x 1 e 2 - ∫ 1 e 2 2 x 3 + 1 d x
= 8 e 3 + 9 e 2 + 13 9
Đáp án D

Đáp án A.
Đơn vị dài là 2 cm vậy nên đơn vị diện tích quy đổi ra sẽ là 2 2 = 4 c m .
Khi đó S = − 1 2 x 3 d x .4 = 15 c m 2

Ta có
S 1 = ∫ 0 k e x sin x d x ; S 2 = ∫ k π e x sin x d x S = S 1 + S 2 = ∫ 0 π e x sin x d x
2 S 1 + 2 S 2 - 1 = 2 S 1 - 1 2
⇔ S 2 = 2 S 1 2 - 2 S 1 + 1 - S = 0 ⇔ 2 ∫ 0 k e x sin x d x 2 - 2 ∫ 0 k e x sin x d x + 1 - ∫ 0 k e x sin x d x = 0
Tính toán trực tiếp qua các đáp án ta thấy PT trên đúng với k = π 2
Đáp án cần chọn là B
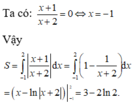
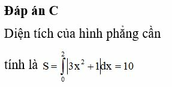
Chọn A