Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

e: Để 4n+1/3n-1 là số nguyên thì \(12n+3⋮3n-1\)
\(\Leftrightarrow3n-1\in\left\{1;-1;7;-7\right\}\)
hay \(n\in\left\{0;-2\right\}\)

Giải:
A = (4n + 5) / (5n + 4)
Giả sử (4n + 5) và (5n + 4) đều chia hết số nguyên tố d
=> 5(4n + 5) - 4(5n + 4) chia hết cho d
Mà 5(4n + 5) - 4(5n + 4) = 9
=> 9 chia hết cho d
=> d có thể là số 3 ( vì d là số nguyên tố)
Nếu (5n + 4) chia hết cho 3 thì (4n + 5) cũng sẽ chia hết cho 3
nên ta chỉ cần xét (5n + 4) chia hết cho 3
♥ xét trường hợp (5n + 4) chia hết cho 3
Do (5n + 4) chia hết cho 3
=> [ (5n + 4) + 6 ] chia hết cho 3 ( vì 6 cũng chia hết cho 3)
=> [ 5(n + 2) ] chia hết cho 3
=> (n + 2) chia hết cho 3 ( do 5 không chia hết cho 3)
=> (n + 2) = 3k ( với k thuộc N )
=> n = 3k - 2 ( với k thuộc N )
Vậy : n = 3k - 2 ( với k thuộc N ) thì A có thể rút gọn được.
+++++++++++
Thử lại xem . Ví dụ : cho k = 2 => n = 4
=> A = (4.4 + 5) / (5.4 + 4) = 21/24
A có thể rút gọn : A = 7/8
♪_♫ Một phân số chỉ có thể rút gọn khi Ước số chung của mẫu số và tử số khác 1 và -1

a: \(-\dfrac{6}{13}=-\dfrac{12}{26}=\dfrac{-18}{39}=-\dfrac{24}{52}=\dfrac{-30}{65}=\dfrac{-36}{78}=\dfrac{-42}{91}\)
b: \(\dfrac{15}{-7}=\dfrac{-15}{7}=\dfrac{-30}{14}=\dfrac{-45}{21}=\dfrac{-60}{28}=\dfrac{-75}{35}=-\dfrac{90}{42}\)



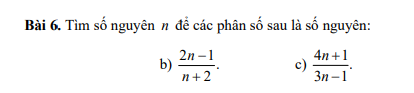

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)