Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx
Hàm số nghịch biến trên R
![]()
Trường hợp 1: m= -1/ 2 ; ta có 0 ≤ 7 2 ∀ x ∈ ℝ
Vậy hàm số luôn nghịch biến trên R.
Trường hợp 2: m< -1/ 2 ; ta có
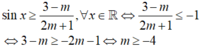
Trường hợp 3:m > -1/2 ; ta có:
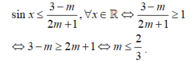
Vậy - 4 ≤ m ≤ 2 3

Chọn A
Tập xác định: D = R.
![]()
Để hàm số nghịch biến trên R thì
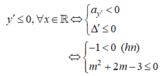
![]()

Chọn C.
y ' = 4 x 3 + 2 x 1 - m = 2 x 2 x 2 + 1 - m
Hàm số nghịch biến trên (-1; 0) nếu y ' < 0, ∀ x ∈ (-1;0)
![]()
![]()
![]()
Dễ thấy hàm số f x = 2 x 2 + 1
![]()
nên y = f (x) nghịch biến trên (-1; 0)
![]()
Vậy để m < 2x 2 + 1, ∀ x ∈ - 1 ; 0 thì m ≤ 1.

Chọn A.
Tập xác định: D = R.
Ta có ![]()
Để hàm số nghịch biến trên R thì
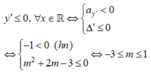

Chọn D.
![]()
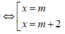
Do đó ta có bảng biến thiên sau:
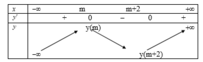
Để hàm số nghịch biến trên khoảng (-1;1) thì
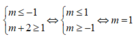

Chọn: D
![]()
Ta có: y ' = m 2 - m - 2 x + m 2
Để hàm số nghịch biến trên khoảng 1 ; + ∞ thì

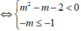
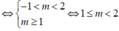
Vậy m ∈ [ 1 ; 2 )

 .
.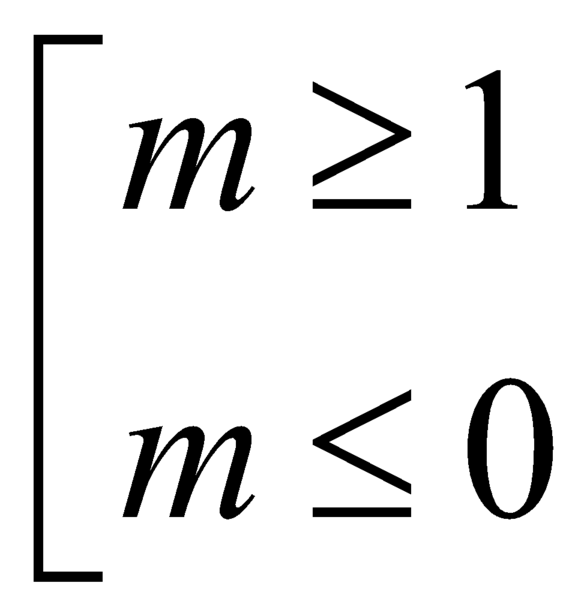 .
.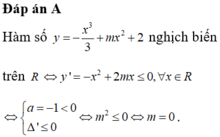
Đáp án A
Bài toán đưa về
sao lại cho g(-1) và cho g(1) vào vậy ạ