Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi ba chữ số của số đó theo thứ tự hàng trăm, hàng chục, hàng đơn vị là a, b, c (0 < a ≤ 9; 0 ≤ b, c ≤ 9). Ta được hệ phương trình
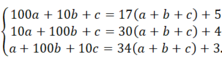
Giải hệ phương trình này tốn nhiều thời gian, không đáp ứng yêu cầu của một bài trắc nghiệm.
Do đó ta phải xét các phương án
- Với phương án A, tổng các chữ số là 10, do đó chia 172 cho 10 được thương là 17 và dư là 2 nên phương án A bị loại.
- Với phương án B, tổng các chữ số là 17. Đổi chữ số hàng trăm cho chữ số hàng chục ta được số 926, số này chia cho 17 không thể có thương là 30, nên phương án B bị loại.
- Với phương án D, nếu đổi chữ số hàng trăm với chữ số hàng chục ta được 857, chia số này cho tổng các chữ số là 20 không thể có thương là 34 nên phương án D bị loại.
Đáp án: C

Gọi số cần tìm là ab
Vì số đó gấp 12 lần hiệu 2 chữ số của nó và chữ số hàng đơn vị lớn hơn chữ số hàng chục nên ta có
ab=12(b-a)
10a+b=12b-12a
11b=22a
b=2a
cho a=1 => b=2
a=2=> b=4
a=3=> b=6
a=4=>b=8
vậy các số cần tìm là 12;24;36;48
Gọi số cần tìm là ab(b>a)
Ta có: ab=12(b-a)
10a+b=12b-12a
10a+12a=12b-b
22a=11b
2a=b
mà ab là số có 2 chữ số
nên a=1;b=2
a=2;b=4
a=3;b=6
a=4;b=8
Vậy các số cần tìm là: 12;24;36;48

Để cho dễ tính toán, ta coi như việc chọn 2 số là theo thứ tự
Không gian mẫu: \(A_{90}^2\)
Chọn số thứ nhất: \(C_{90}^1=90\) cách
Hàng đơn vị số thứ 2 có 1 cách chọn (giống hàng đơn vị số thứ nhất), hàng chục số thứ 2 có 8 cách chọn (khác hàng chục số thứ hai và 0)
\(\Rightarrow90.1.8\) cách chọn 2 số thỏa mãn yêu cầu
Xác suất: \(P=\dfrac{90.1.8}{A_{90}^2}\)

\(\overline{abcdef}\)
c,d,e có thể lấy bộ ba (1;2;5); (1;3;4)
TH1: c,d,e lấy bộ ba (1;2;5)
a có 6 cách
b có 5 cách
f có 4 cách
c,d,e có 3!=6 cách
=>Có 6*6*5*4=36*20=720(số)
TH2: c,d,e lấy bộ ba 1;3;4
a có 6 cách
b có 5 cách
f có 4 cách
c,d,e có 3!=6 cách
=>Có 6*6*5*4=36*20=720(số)
=>Có 720+720=1440 số