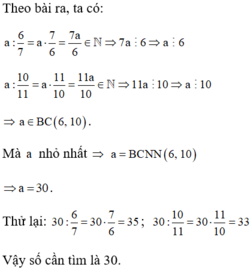Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Gọi số phải tìm là a, a ∈ N*
Vì a chia cho 6, 7, 9 được số dư lần lượt là 2, 3, 5 nên (a+4) chia hết cho 6,7,9.
Suy ra (a+4) ∈ BC(6,7,9)
Mà a là số tự nhiên nhỏ nhất
Suy ra (a+4) = BC(6,7,9) = 3 2 . 2 . 7 = 126 => a+4 = 126 => a = 122
Vậy số phải tìm là 126
b, Gọi số phải tìm là a, a ∈ N*
Vì a chia cho 17, 25 được các số dư theo thứ tự là 8 và 16.
nên (a+7) chia hết cho 8; 16.
Suy ra (a+7) ∈ BC(8;16)
Suy ra BCNN(8;16) = 16 => a+7 ∈ B(16) = 16k (k ∈ N).
Vậy số phải tìm có dạng 16k – 7

6/7 = 7a/6 Mà ƯCLN ( 7 ; 6 ) = 1 nên a thuộc B ( 6 )
a : 10/11 = 11a/10 Mà ƯCLN ( 11 ; 10 ) = 1 nên a thuoccj B ( 10 )
Để a nhỏ nhất <=> a = BCNN ( 6 ; 10 ) = 30

Theo bài ra, ta có:
+a : \(\frac{6}{7}\) =\(\frac{7a}{6}\) thuộc N => 7a chia hết cho 6
Mà UCLN(7,6)=1 => a chia hết cho 6 (1)
+a : \(\frac{10}{11}\) = \(\frac{11a}{10}\) thuộc N => 11a chia hết cho 10
Mà UCLN(11, 10) =1 => a chia hết cho 10 (2)
Từ (1) và (2) => a thuộc BC(10,6)
Mà a nhỏ nhất => a =BCNN(10,6) => a =30
Vậy số cần tìm là 30
k cho mình nha

a/(6/7) = 7a/6;
a/(10/11) = 11a/10;
vì 7 không chia hết cho 6 nên a phải chia hết cho 6
vì 11 không chia hết cho 10 nên a phải chia hết cho 10
mà a nhỏ nhất
=> a là bcnn(6,10) => a=60
Theo đề bài a :6/7 = a . 7/6 thuộc N nên 7a chia hết cho 6 nên suy ra a chia hết cho 6 (vì 7 và 6 nguyên tố cùng nhau): a : 10/11 = a. 11/10 thuộc N nên 11a chia hết cho 10 suy ra a chia hết cho 10 ( vì 11 và 10 nguyên tố cùng nhau). Như vậy a là bội chung của 6 và 10.
Để a nhỏ nhất thì a = BCNN (6 ;10) = 30
Vậy số phải tìm là 30