Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đặt: \(t^2=x^2+x+6\)
=> \(4t^2=4x^2+4x+24=\left(2x+1\right)^2+23\)
=> \(4t^2-\left(2x+1\right)^2=23\)
<=> \(\left(2t-2x-1\right)\left(2t+2x+1\right)=23\)
Chia các trường hợp: => x và t
A là số chính phương, suy ra
\(x^2-6x+6=k^2\) \(\left(k\inℕ\right)\)
\(\Leftrightarrow\left(x-3\right)^2-3=k^2\Leftrightarrow\left(x-3\right)^2-k^2=3\Leftrightarrow\left(x-3-k\right)\left(x-3+k\right)=3\)
Vì \(x;k\inℕ\Rightarrow x-3-k< x-3+k\)nên ta có các trường hợp sau
\(\hept{\begin{cases}x-3-k=1\\x-3+k=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=5\left(tm\right)\\k=1\end{cases}}\)
\(\hept{\begin{cases}x-3-k=-3\\x-3+k=-1\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\left(ktm\right)\\k=1\end{cases}}}\)
Vậy x=5 thì giá trị biểu thức A là số chính phương
A = x2 - 6x + 6
= x2 - 2.x.3 + 32 - 3
=(x - 3)2 - 3
Ta có: \(\left(x-3\right)^2\ge0\forall x\)=> (x - 3)2 - 3 < 0 =>A < 0 =>A không là số chính phương(vì số chính phương luôn lớnhơnhoặc bằng0)
=> \(x\in\varnothing\)
Vậy không có số nguyên tố x nào thỏa mãn đề bài
Điều kiện xác định của phân thức: n ≠ 2
Ta có:
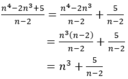
Vậy để N nguyên thì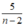 
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì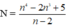 
có giá trị là số nguyên
Xét p=2,p=2, ta có: 4p+1=94p+1=9 là số chính phương.
Xét p>2,p>2, vì pp là số nguyên tố nên p=2k+1p=2k+1 (k∈N∗)(k∈N∗)
Ta có: 4p+1=4(2k+1)+1=8k+54p+1=4(2k+1)+1=8k+5
Mặt khác 4p+14p+1 là một số chính phương lẻ nên chia 88 dư 1.1.
Do đó với p>2p>2 thì 4p+14p+1 không là số chính phương.
Vậy số nguyên tố pp để 4p+14p+1 là số chính phương là 2.2.
Xét p=2 , ta có : 4p + 1 = 9 là số chính phương
Xét p > 2 , vì p là số nguyên tố nên p = 2k + 1 (k thuộc N*)
Ta có : 4p + 1 = 4(2k + 1) +1 = 8k + 5
Mặt khác 4p + 1 là một số chính phương lẻ nên chia 8 dư 1
Do đó với p > 2 thì 4p + 1 ko là số chính phương
Vậy số nguyên tố p để 4p + 1 là số chính phương là 2
