Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1, 32 < 2^n < 128
2^5 < 2^n < 2^7
=> 5 < n < 7
Vì n là nguyên dương => n = 6
2, 2.16 > (=) 2^n > 4
2.2^4 > (=) 2^n > 2^2
2^5 > (=) 2^n > 2^2
5 >(=) n > 2 => n = 5 ; 4 ; 3
3, 9.27 < 3^n <= 243
3^2 . 3^3 < 3^n <= 3^5
3^5 < 3^n <=5
5 < n <= 5 ( không có n)

Bài 5:
a) \(32< 2^n< 128\)
⇔ \(2^5< 2^n< 2^7\)
⇔ \(5< n< 7\)
=> \(n=6\)
Vậy \(n=6.\)
b) Sửa lại đề là \(2.16>2^n>4\)
⇔ \(32>2^n>4\)
⇔ \(2^5>2^n>2^2\)
⇔ \(5>n>2\)
=> \(n=3;n=4\)
Vậy \(n\in\left\{3;4\right\}.\)
c) \(9.27< 3^n< 243\)
⇔ \(243< 3^n< 243\)
⇔ \(3^5< 3^n< 3^5\)
⇔ \(5< n< 5\)
=> \(n\in\varnothing\)
Vậy không tồn tại giá trị nào của \(n.\)
Mình chỉ làm bài 5 thôi nhé.
Chúc bạn học tốt!
5.
a) 32 < 2n < 128
<=> 25 < 2n < 27
<=> 2n = 26
<=> n = 6
b) sai đề
c) 9.27 \(\le\) 3n \(\le\) 243
<=> 35 \(\le\) 3n \(\le\) 35
<=> 3n = 35 <=> n = 5
6.
a) 9920 = (992)10 = 980110
Vì 9801 < 9999 nên 980110 < 999910
hay 9920 < 999910
b) 321 = 3.320 = 3.(32)10 = 3.910
231 = 2.230 = 2.(23)10 = 2.810
Vì 3.910 < 2.810 nên 321 < 231
c) 3.2410 = 3.(23.3)10 = 311.230 = 311.(22)15 = 311.415
Vì 311.415 < 415.415 = 430
nên 3.2410 < 230 + 330 + 430

a) ta có 2.16\(\ge\)2n > 4
\(\rightarrow\)2.24\(\ge\)2n>22
\(\rightarrow\) 25\(\ge\)2n>22
\(\Rightarrow\) n\(\in\){ 3;4;5}
b) làm tương tự

a) 32 < 2^n < 128
hay 2^5 < 2^n < 2^7
=> 5 < n < 7
=> n = 6
b) 2.16 \(\ge\)2^n > 4
hay 2^5 \(\ge\)2^n > 2^2
=> 5 \(\ge\)n > 2
=> n \(\in\left\{5;4;3\right\}\)
c) 9.27 \(\le\)3^n \(\le\) 243
hay 3^5 \(\le\)3^n \(\le\) 3^5
=> 5 \(\le\) n \(\le\) 5
=> n = 5
a,32<2^n<128
n sẽ bằng 6 vì khi 2^6=64>32 và 2^6=64 <128 (thỏa mãn điều kiện)
Vậy :n=6
lm tương tự
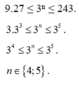
a) \(2\cdot16\ge2^n>4\\ 2\cdot2^4\ge2^n>2^2\\ 2^5\ge2^n>2^2\\ \Rightarrow2^n\in\left\{2^3;2^4;2^5\right\}\\ \Rightarrow n\in\left\{3;4;5\right\}\)Vậy \(n\in\left\{3;4;5\right\}\)
b) \(9\cdot27\le3^n\le243\\ 3^2\cdot3^3\le3^n\le3^5\\ 3^5\le3^n\le3^5\\ \Rightarrow3^n=3^5\\ \Rightarrow n=5\)Vậy n = 5
a) \(2.16\ge2^n>4\)
\(\Rightarrow32\ge2^n>4\)
\(\Rightarrow2^5\ge2^n>2^2\)
\(\Rightarrow5\ge n>2\)
\(\Rightarrow\left\{{}\begin{matrix}n=3\\n=4\\n=5\end{matrix}\right.\)
Vậy \(n\in\left\{3;4;5\right\}.\)
b) \(9.27\le3^n\le243\)
\(\Rightarrow243\le3^n\le243\)
\(\Rightarrow3^5\le3^n\le3^5\)
\(\Rightarrow5\le n\le5\)
\(\Rightarrow n=5\)
Vậy \(n=5.\)
Chúc bạn học tốt!