CN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KT
1 tháng 3 2021
1) n4 + 4 = (n4 + 4n2 + 4) - 4n2 = (n2 + 2)2 - (2n)2 = (n2 + 2 + 2n).(n2 + 2 - 2n)
Ta có n2 + 2n + 2 = (n+1)2 + 1 > 1 với n là số tự nhiên
n2 - 2n + 2 = (n -1)2 + 1 1 với n là số tự nhiên
Để n4 + 4 là số nguyên tố => thì n4 + 4 chỉ có 2 ước là chính nó và 1
=> n2 + 2n + 2 = n4 + 4 và n2 - 2n + 2 = (n -1)2 + 1 = 1
(n -1)2 + 1 = 1 => n - 1= 0 => n = 1
Vậy n = 1 thì n4 là số nguyên tố
TH
1
21 tháng 3 2018
copy cái bài trên mạng ak :) có đáp án rồi mờ :) đăng lên làm j ? :))
NM
Nguyễn Minh Quang
Giáo viên
17 tháng 8 2021
a.\(n^4+4=n^4+4n^2+4-4n^2=\left(n^2+2\right)^2-\left(2n\right)^2=\left(n^2+2n+2\right)\left(n^2-2n+2\right)\)
nguyên tố nên thừa số nhỏ hơn là \(n^2-2n+2=1\Leftrightarrow\left(n-1\right)^2=0\Leftrightarrow n=1\)thỏa mãn đề bài
b. ta có :\(n^{1994}+n^{1993}+1-\left(n^2+n+1\right)=\left(n^{1992}-1\right)\left(n^2+n\right)\)
mà \(1992⋮3\Rightarrow n^{1992}-1⋮n^3-1⋮n^2+n+1\)
nên \(n^{1994}+n^{1993}+1⋮n^2+n+1\)mà nó là số nguyên tố nên
\(n^2+n+1=1\Leftrightarrow n=0\) ( Do n là số tự nhiên nên n= -1 loại bỏ đi )
PT
1
CM
4 tháng 11 2019
Điều kiện xác định của phân thức: n ≠ 2
Ta có:
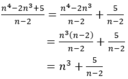
Vậy để N nguyên thì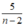 
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì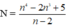 
có giá trị là số nguyên
TV
1
4 tháng 12 2021
\(n^4+64=n^4+16n^2+64-16n^2\)
\(=\left(n^2+8\right)^2-\left(4n\right)^2\)
\(=\left(n^2-4n+8\right)\left(n^2+4n+8\right)\)
AH
Akai Haruma
Giáo viên
15 tháng 11 2021
Lời giải:
Đặt $n^4+4n^2-1=a^2$ với $a$ là số tự nhiên
$\Leftrightarrow (n^2+2)^2-5=a^2$
$\Leftrightarrow 5=(n^2+2)^2-a^2=(n^2+2-a)(n^2+2+a)$
Do $n^2+2+a\geq n^2+2-a$ với $a\geq 0$ và $n^2+2+a>0$ nên:
$n^2+2+a=5$ và $n^2+2-a=1$
$\Rightarrow 2(n^2+2)=6\Rightarrow n^2+2=3$
$\Leftrightarrow n^2=1$
$\Rightarrow n=\pm 1$
a) Cần chứng minh : \(a^4-1\)chia hết cho 5 với mọi a là số tự nhiên.
Thật vậy : Với mọi số tự nhiên a không chia hết cho 5, sẽ có một trong các dạng : \(a=5k\pm1,a=5k\pm2\)(k thuộc N)
\(a^2\)có một trong hai dạng \(5k+1\)hoặc \(5k+4\)
\(a^4\)có một dạng duy nhất là \(5k+1\). Vậy \(a^4-1⋮5\)với mọi a là số tự nhiên.
Ta biểu diễn : \(A=\left(n^4-1\right)+5\) . Nhận thấy n4-1 chia hết cho 5 , 5 chia hết cho 5 => A chia hết cho 5. Mà A là số nguyên tố, vậy A = 5. Suy ra được n = 1
b) Với n = 1 , dễ thấy B = 5 là số nguyên tố
Với n = 2 , B = 32 không là số nguyên tố.
Với n = 3 , B = 145 không là số nguyên tố
Xét với n là số nguyên tố, n > 3, biểu diễn B dưới dạng : \(B=\left(n^4-1\right)+\left(4^n+1\right)\)
Dễ thấy n4-1 chia hết cho 5 , \(4^n+1=4^n+1^n=\left(4+1\right).M=5M⋮5\)
Suy ra B chia hết cho 5. Mà B là số nguyên tố, vậy B = 5. Vậy n = 1 thỏa mãn đề bài