TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
2
8 tháng 11 2015
a) n2+12n = n(n+12) là số nguyên tố
Mà nếu n là hợp số thì n(n+12) là hợp số
Mà nếu n là số nguyên tố thì n(n+12) là hợp số (chia hết cho n)
=> n không phải là hợp số và số nguyên tố
=> n = 0 hoặc n = 1
Mà nếu n = 0 thì n2+12n = 0 => loại
n = 1 => n2+12n = 13 =>chọn
Vậy n = 1
AH
Akai Haruma
Giáo viên
25 tháng 2 2023
Lời giải:
$n^2+12n=n(n+12)$ nên để $n^2+12n$ là số nguyên tố thì 1 trong 2 thừa số $n, n+12$ bằng $1$, số còn lại là số nguyên tố.
Mà $n< n+12$ nên $n=1$
Khi đó: $n^2+12n=1^2+12.1=13$ là số nguyên tố (thỏa mãn)
NT
1
12 tháng 7 2016
Tìm tất cả các số tự nhiên n để :
a/ n^2 +12n là số nguyên tố
b/ 3^n +6 là số nguyên tố
TT
0
PH
0
TL
0
HT
7
TM
27 tháng 10 2016
a) \(n^2+12n=n\left(n+12\right)\)
- \(n\ge1\)
- \(n+12\ge13\)
Để n2+12n nguyên tố thì n2+12n chỉ có 2 ước là 1 và chính nó
\(\Rightarrow\hept{\begin{cases}n=1\\n+12=n^2+12n\end{cases}}\)
Vậy n=1
b)\(3^n+6=3\left(3^{n-1}+6\right)\) với \(3^{n-1}+6\ge1\)
Để 3n+6 là số nguyên tố thì 3n+6 chỉ có ước là 1 và chính nó
=>\(\hept{\begin{cases}3^n+6=3\\3^{n-1}+6=1\end{cases}}\)=> Không có số n thỏa mãn
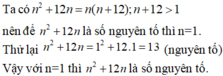
a)
Xét n =0
=> 3n+6 = 30+6 = 1+6 = 7 ( là số nguyên tố )
Xét n \(\ne\)0
=> 3n+ 6 = 3.(3n-1+2) chia hết cho 3 ( là hợp số )
Vay n=0
b)
n2+12n = n(n+12)
Xét n =0 => n(n+12) = 0 (vô lý )
Xét n = 1 => n(n+12) = 1.13 =13 ( là số nguyên tố )
Xét n >1
=> n(n+12) chia hết cho n ; (n+12 ) (la hop so )
Vậy n =1