Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3 câu này bạn áp dụng cái này nhé.
`a^2 >=0 forall a`.
`|a| >=0 forall a`.
`1/a` xác định `<=> a ne 0`.
a: P=(x+30)^2+(y-4)^2+1975>=1975 với mọi x,y
Dấu = xảy ra khi x=-30 và y=4
b: Q=(3x+1)^2+|2y-1/3|+căn 5>=căn 5 với mọi x,y
Dấu = xảy ra khi x=-1/3 và y=1/6
c: -x^2-x+1=-(x^2+x-1)
=-(x^2+x+1/4-5/4)
=-(x+1/2)^2+5/4<=5/4
=>R>=3:5/4=12/5
Dấu = xảy ra khi x=-1/2

Câu hỏi của đào mai thu - Toán lớp 7 - Học toán với OnlineMath
eM THAM khảo nhé!

Ta có: \(\left\{{}\begin{matrix}\left|x-3\right|\ge0\forall x\\\left|y+3\right|\ge0\forall y\end{matrix}\right.\)
+) \(\left|x-3\right|\ge0\Rightarrow\left(\left|x-3\right|+2\right)\ge2\)
\(\Rightarrow\left(\left|x-3\right|+2\right)^2\ge4\)
Dấu ''='' xảy ra \(\Leftrightarrow x=3\)
=> \(Min_{\left(\left|x-3\right|+2\right)^2}=4\Leftrightarrow x=3\)
+) \(\left|y+3\right|\ge0\)
Dấu ''='' xảy ra \(\Leftrightarrow y=-3\)
=> \(Min_{\left|y+3\right|}=0\Leftrightarrow y=-3\)
\(\Rightarrow MIN_Q=4+0+2017=2021\)
Vậy \(MIN_Q=2021\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\)

1. a) Ta có: M = |x + 15/19| \(\ge\)0 \(\forall\)x
Dấu "=" xảy ra <=> x + 15/19 = 0 <=> x = -15/19
Vậy MinM = 0 <=> x = -15/19
b) Ta có: N = |x - 4/7| - 1/2 \(\ge\)-1/2 \(\forall\)x
Dấu "=" xảy ra <=> x - 4/7 = 0 <=> x = 4/7
Vậy MinN = -1/2 <=> x = 4/7
2a) Ta có: P = -|5/3 - x| \(\le\)0 \(\forall\)x
Dấu "=" xảy ra <=> 5/3 - x = 0 <=> x = 5/3
Vậy MaxP = 0 <=> x = 5/3
b) Ta có: Q = 9 - |x - 1/10| \(\le\)9 \(\forall\)x
Dấu "=" xảy ra <=> x - 1/10 = 0 <=> x = 1/10
Vậy MaxQ = 9 <=> x = 1/10

\(\left|x-3\right|+2>=2\)
=>(|x-3|+2)^2>=4
\(A=\left(\left|x-3\right|+2\right)^2+\left|y+3\right|+2018>=4+2018=2022\)
Dấu = xảy ra khi x-3=0 và y+3=0
=>x=3 và y=-3
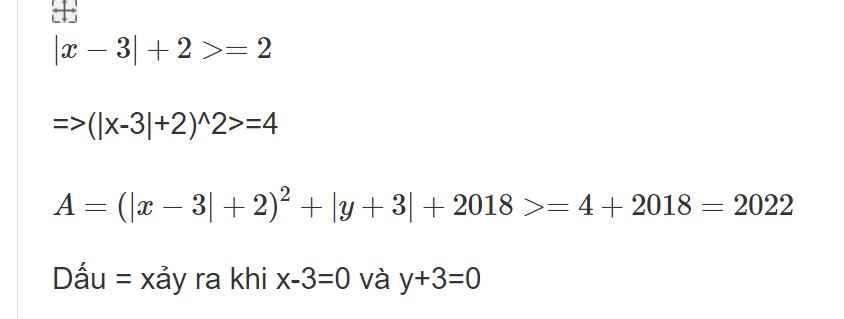
Ta có: \(\left(\left|x-3\right|+2\right)^2\ge0\forall x\) không âm
\(\left|y+3\right|\ge3\forall y\) không âm
Cộng theo vế 2 BĐT trên ta có:
\(A=\left(\left|x-3\right|+2\right)^2+\left|y+3\right|+2018\ge0+3+2018=2021\)
Vậy \(A_{min}=2021\Leftrightarrow\hept{\begin{cases}\left(\left|x-3\right|+2\right)^2=0\\\left|y+3\right|=3\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=0\end{cases}}}\)