KC
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 7 2017
B = x2y2+2x2+24xy+16x+191 = [ (xy)^2 + 24xy + 144] + \(\left[\left(\sqrt{2}x\right)^2+2.\sqrt{2}x.4\sqrt{2}+32\right]\)+15
= (xy+12)^2 +(\(\sqrt{2}x\)+\(4\sqrt{2}\))^2 + 15
( ở đây mik làm tắt) => Min B = 15 khi \(\sqrt{2}x+4\sqrt{2}=0=>x=-4\)và xy+12 = 0 => -4y = -12= > y=3
25 tháng 7 2017
A= 2x^2+9y^2-6xy-6x-12y+2004
A = (x^2 -6xy +9y^2) + 4(x -3y) + x^2 - 10x + 2004
A = [(x -3y)^2 +4(x -3y) + 4] + (x^2 -10x +25) + 1975
A= (x -3y +2)^2 + (x -5)^2 + 1975
( mik rút mấy cái bước (x-3y+2)^2 = 0, bn làm thì nên thêm vào=> Min A = 1975 vs x= 5 và y = 7/3
D=-x^2+2xy-4y^2+2x+10y-8
D = (-x^2 - y^2 - 1 + 2xy + 2x - 2y) + (-3y^2 + 12y - 12) + 5
D = -(x^2+y^2+1 - 2xy - 2x + 2y) - 3(y^2 - 4y + 4) + 5
D= - (x - y - 1)^2 - 3(y - 2)^2 +5
=> Max D = 5 khi x= 3 và y=2
26 tháng 9 2017
\(C=-x^2+2xy-4y^2+2x+10y-3\)
\(=-\left(x^2+2xy-y^2\right)+2x-2y-1-3y^2+12y-12+10\)
\(=-\left(x-y\right)^2+2\left(x-y\right)-1-3\left(y^2-4y+4\right)+10\)
\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+10\le10\forall x;y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=3\\y=2\end{cases}}}\)
Vậy \(C_{max}=10\) tại x = 3; y = 2
28 tháng 8 2018
\(A=-x^2+2xy-4y^2+2x+10y-8\)
\(=-\left(x^2-2xy+4y^2-2x-10y+8\right)\)
\(=-\left[\left(x-y-1\right)^2+3\left(y-2\right)^2-5\right]\)
\(=5-\left(x-y-1\right)^2-3\left(y-2\right)^2\le5\)
Dấu"=" xảy ra <=> \(\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}}\) <=> \(\hept{\begin{cases}x=3\\y=2\end{cases}}\)
Vậy MAX \(A=5\)khi \(x=3;\)\(y=2\)
BS
1
26 tháng 6 2019
\(A=-x^2+2xy-4y^2+2x+10y-8\)
\(=-x^2+2xy-y^2-3y^2+2x-2y+12y-12+4\)
\(=-\left(x^2-2xy+y^2\right)+\left(2x-2y\right)-1-\left(3y^2-12y+12\right)+5\)
\(=-\left(x-y\right)^2+2\left(x-y\right)-1-3\left(y-2\right)^2+5\)
\(=-\left[\left(x-y\right)^2-2\left(x-y\right)+1\right]\)\(-3\left(y-2\right)^2+5\)
\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+5\)
\(A_{max}=5\Leftrightarrow\hept{\begin{cases}\left(x-y-1\right)^2=0\\3\left(y-2\right)^2=0\end{cases}\Rightarrow\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}x-y-1=0\\y=2\end{cases}}\)\(\Rightarrow x-2-1=0\Leftrightarrow x=3\)
\(KL:A_{max}=5\Leftrightarrow x=3;y=2\)
TM
15 tháng 7 2017
\(C=-3x\left(3+x\right)-7=-9x-3x^2-7=-\left(3x^2+9x+7\right)=-3\left(x^2+3x+\frac{7}{3}\right)\)
=\(-3\left(x^2+2.\frac{3}{2}.x+\frac{9}{4}+\frac{1}{12}\right)=-3\left[\left(x+\frac{3}{2}\right)^2+\frac{1}{12}\right]=-3\left(x+\frac{3}{2}\right)^2-\frac{1}{4}\le-\frac{1}{4}\)
Dấu "=" xảy ra khi x=-3/2
---
\(D=2xy-x^2-4y^2-8+2x+10y\)
\(=-\left(x^2+2xy-2x+4y^2-10y+8\right)\)
\(=-\left[x^2+2x\left(y-1\right)+4y^2-10y+8\right]\)
\(=-\left[x^2+2x\left(y-1\right)+\left(y^2-2y+1\right)+3y^2-8y+7\right]\)
\(=-\left[x^2+2x\left(y-1\right)+\left(y-1\right)^2+3\left(y^2-2.\frac{4}{3}.y+\frac{16}{9}\right)+\frac{5}{3}\right]\)
\(=-\left[\left(x+y-1\right)^2+3\left(y-\frac{4}{3}\right)^2+\frac{5}{3}\right]\)
\(=-\left(x+y-1\right)^2-3\left(y-\frac{4}{3}\right)^2-\frac{5}{3}\le-\frac{5}{3}\)
Dấu "=" xảy ra khi x=-1/3 và y=4/3
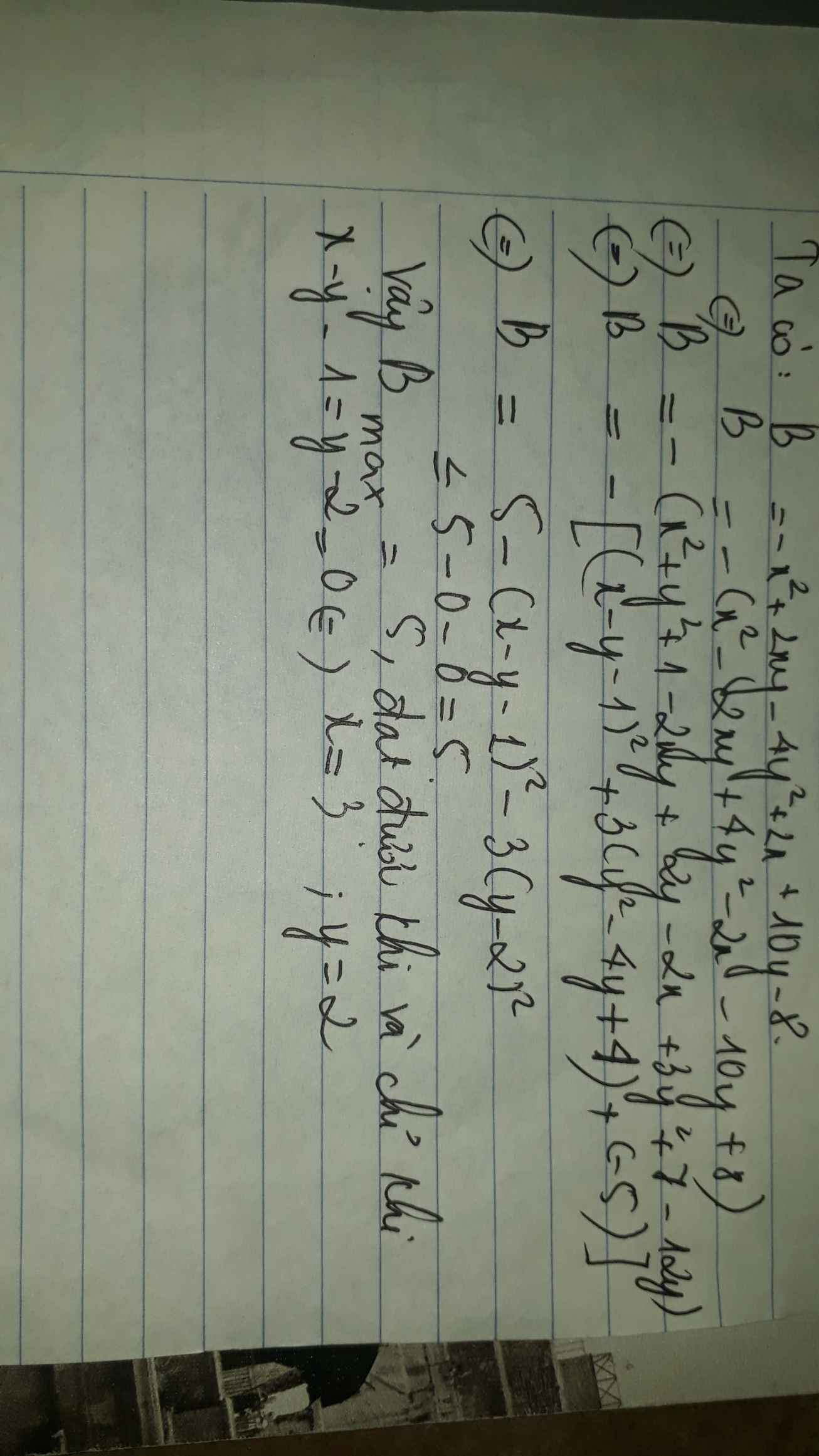
-A= x^2-2xy+4y^2-2x-10y+8
-A= ( x^2+y^2+1-2xy-2x+2y) +(3y^2-12y+7)
-A=(x-y-1)^2+ 3(y^2-4y+7/4)=(x-y-1)^2+3(y-2)^2-27/4>=-... nen A<= 27/4
(ko biết có đúng hay ko)
-A= x^2-2xy+4y^2-2x-10y+8
-A= ( x^2+y^2+1-2xy-2x+2y) +(3y^2-12y+7)
-A=(x-y-1)^2+ 3(y^2-4y+7/4)=(x-y-1)^2+3(y-2)^2-27/4>=-... nen A<= 27/4