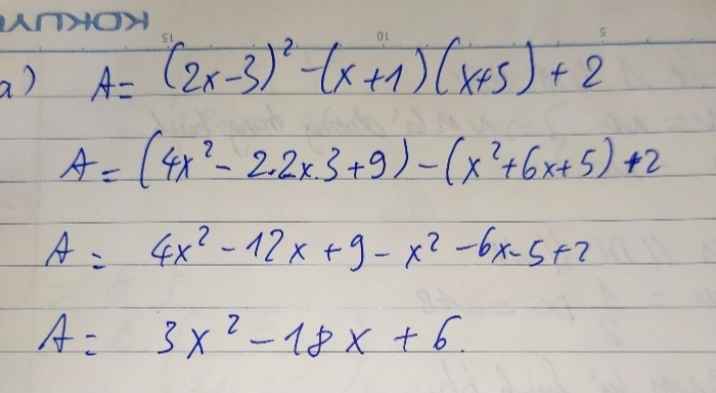NT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 5 2020
\(A=\left[\frac{6x^2}{x^3-1}-\frac{2x-2}{x^2+x+1}-\frac{1}{x-1}\right]:\frac{x^2+9}{\left(x-1\right)\left(9-4x\right)}\)
\(=\left[\frac{6x^2}{x^3-1}-\frac{\left(2x-2\right)\left(x-1\right)}{\left(x^2+x+1\right)\left(x-1\right)}-\frac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\right]\cdot\frac{\left(x-1\right)\left(9-4x\right)}{x^2+9}\)
\(=\frac{6x^2-\left(2x^2-4x+2\right)-x^2-x-1}{\left(x^2+x+1\right)\left(x-1\right)}\cdot\frac{\left(x-1\right)\left(9-4x\right)}{x^2+9}\)
\(=\frac{5x^2-2x^2+4x-2-x-1}{\left(x^2+x+1\right)}\cdot\frac{\left(9-4x\right)}{x^2+9}\)
\(=\frac{3x^2+3x-3}{\left(x^2+x+1\right)}\cdot\frac{\left(9-4x\right)}{x^2+9}\)
Biểu thức A bạn viết đúng chưa?
14 tháng 12 2017
\(A=\frac{3x^2+8x+6}{x^2+2x+1}\) \(\left(x\ne\pm1\right)\)
\(A=\frac{\left(3x^2+6x+3\right)+\left(2x+3\right)}{\left(x+1\right)^2}\)
\(A=\frac{3\left(x+1\right)^2+2x+3}{\left(x+1\right)^2}\)
\(A=3+\frac{2x+3}{\left(x+1\right)^2}\)
Vì\(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow3+\frac{2x+3}{\left(x+1\right)^2}\ge3\Leftrightarrow A\ge3\)
Dấu "="xảy ra khi \(2x+3=0\Rightarrow x=\frac{-3}{2}\)
LM
14 tháng 12 2017
Gọi k là một giá trị của A ta có:
\(\frac{\left(3x^2-8x+6\right)}{\left(x^2+2x+1\right)}=k\)
\(\Leftrightarrow3x^2-8x+6=k\left(x^2-2x+1\right)\)
\(\Leftrightarrow\left(3-k\right)x^2-\left(8-2k\right)x+6-k=0\)(*)
Ta cần tìm k để PT (*) có nghiệm
Xét: \(\Delta=\left(8-2k\right)^2-4\left(3-k\right)\left(6-k\right)=64-32k+4k^2-4\left(18-9k+k^2\right)=4k-8\)
Để PT (*) có nghiệm thì: \(\Delta\ge0\Leftrightarrow4k-8\ge0\Leftrightarrow k\ge2\)
Dấu "=" xảy ra khi: \(-\left(8-2.2\right)x+6-2=0\Leftrightarrow-4x+4=0\Rightarrow x=1\)
Vậy: \(B\ge2\)suy ra: B = 2 khi x = 1
5 tháng 8 2019
Ta có: A = x2 - 5x + 1 = (x2 - 5x + 25/4) - 21/4 = (x - 5/2)2 - 21/4
Ta luôn có: (x - 5/2)2 \(\ge\)0 \(\forall\)x
=> (x - 5/2)2 - 21/4 \(\ge\)-21/4 \(\forall\)x
Dấu "=" xảy ra <=> x -5/2 = 0 <=> x = 5/2
Vậy Min A = -21/4 tại x = 5/2
Ta có: B = -x + 3x + 1 = -(x - 3x + 9/4) + 13/4 = -(x - 3/2)2 + 13/4
Ta luôn có: -(x - 3/2)2 \(\le\)0 \(\forall\)x
=> -(x - 3/2)2 + 13/4 \(\le\)13/4 \(\forall\)x
Dấu "=" xảy ra <=> x - 3/2 = 0 <=> x = 3/2
Vậy Max B = 13/4 tại x = 3/2
(xem lại đề)
19 tháng 7 2017
\(P=\frac{\left(\frac{1}{4}x^2-\frac{1}{2}x+\frac{1}{4}\right)+\left(\frac{3}{4}x^2+\frac{3}{2}x+\frac{3}{4}\right)}{x^2-2x+1}=\frac{\frac{1}{4}\left(x-1\right)^2+\frac{3}{4}\left(x+1\right)^2}{\left(x-1\right)^2}=\frac{1}{4}+\frac{\frac{3}{4}\left(x+1\right)^2}{\left(x-1\right)^2}\)
Ta thấy : \(\frac{\frac{3}{4}\left(x+1\right)^2}{\left(x-1\right)^2}\ge0\forall x\) nên \(\frac{1}{4}+\frac{\frac{3}{4}\left(x+1\right)^2}{\left(x-1\right)^2}\ge\frac{1}{4}\forall x\) có GTNN là \(\frac{1}{4}\) tại x = - 1
Vậy \(P_{min}=\frac{1}{4}\) tại \(x=-1\)
19 tháng 7 2017
\(P=\frac{\left(x^2-2x+1\right)+\left(3x-3\right)+3}{\left(x-1\right)^2}=\frac{\left(x-1\right)^2+3\left(x-1\right)+3}{\left(x-1\right)^2}=1+\frac{3}{x-1}+\frac{3}{\left(x-1\right)^2}\)
đặt \(y=\frac{1}{x-1}\Rightarrow P=1+3y+3y^2=3\left(y+\frac{1}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}\)
vậy \(MinP=\frac{1}{4}\Leftrightarrow y=-\frac{1}{2}\Leftrightarrow\frac{1}{x-1}=-\frac{1}{2}\Leftrightarrow x=-1\)
15 tháng 7 2021
`|x-2|=2x-3(x>=3/2)`
`<=>` \(\left[ \begin{array}{l}x-2=2x-3\\x-2=3-2x\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=1(l)\\3x=5\end{array} \right.\)
`<=>x=5/3(Tm(`
`2)A=-x^2+2x+9`
`=-(x^2-2x)+9`
`=-(x^2-2x+1)+1+9`
`=-(x-1)^2+10<=10`
Dấu "=" xảy ra khi `x=1.`
15 tháng 7 2021
1,
* \(|x-2|=x-2< =>x\ge2\)
\(=>x-2=2x-3< =>x=1\left(ktm\right)\)
*\(\left|x-2\right|=2-x< =>x< 2\)
\(=>2-x=2x-3< =>x=\dfrac{5}{3}\left(tm\right)\)
vậy x=5/3
2, \(A=-x^2+2x+9=-\left(x^2-2x-9\right)=-\left(x^2-2x+1-10\right)\)
\(=-\left[\left(x-1\right)^2-10\right]=-\left(x-1\right)^2+10\le10\)
dấu"=" xảy ra<=>x=1
25 tháng 7 2018
\(x^2\left(2-x^2\right)\)
\(=x^2.2-\left(x^2\right)^2\)
\(=2x^2-\left(x^2\right)^2\)
\(=-x^4+2x^2\)
=> BT ko có GTLN/GTNN
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 7 2021
\(A=4x^2-12x+9-\left(x^2+6x+5\right)+2\)
\(=3x^2-18x+6\)
\(=3\left(x^2-6x+9\right)-21\)
\(=3\left(x-3\right)^2-21\ge-21\)
\(A_{min}=-21\) khi \(x=3\)
19 tháng 7 2021
a) Ta có: \(A=\left(1+\dfrac{x^2}{x^2+1}\right):\left(\dfrac{1}{x-1}-\dfrac{2x}{x^3+x-x^2-1}\right)\)
\(=\dfrac{2x^2+1}{x^2+1}:\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(=\dfrac{2x^2+1}{x^2+1}\cdot\dfrac{\left(x-1\right)\left(x^2+1\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2+1}{x-1}\)
b) Thay \(x=-\dfrac{1}{2}\) vào A, ta được:
\(A=\left(2\cdot\dfrac{1}{4}+1\right):\left(\dfrac{-1}{2}-1\right)\)
\(=\dfrac{3}{2}:\dfrac{-3}{2}=-1\)
c) Để A<1 thì A-1<0
\(\Leftrightarrow\dfrac{2x^2+1}{x-1}-1< 0\)
\(\Leftrightarrow\dfrac{2x^2+1-x+1}{x-1}< 0\)
\(\Leftrightarrow\dfrac{2x^2-x+2}{x-1}< 0\)
\(\Leftrightarrow x-1< 0\)
hay x<1
