Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)

a/
\(\Leftrightarrow cosx=2m-1\)
Do \(-1\le cosx\le1\) nên pt có nghiệm khi và chỉ khi:
\(-1\le2m-1\le1\Rightarrow0\le m\le1\)
b/
Điều kiện để hàm số làm sao bạn?

14) đề bài tương đương với
cotx = -\(\sqrt{3}\Leftrightarrow cotx=cot\left(\frac{-\pi}{6}\right)\Leftrightarrow x=\frac{-\pi}{6}+k\pi\)
16) đề bài tương đương với
cosx=2m-1
ta có cosx \(\in\left[-1;1\right]\Leftrightarrow-1\le2m-1\le1\\ \Leftrightarrow\left\{{}\begin{matrix}2m-1\ge-1\\2m-1\le1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m\le1\end{matrix}\right.\)
vì n là số nguyên nên m=0 hoặc m=1

ĐKXĐ: 2m-3sinx>=0
=>3sin x<=2m
=>sin x<=2m/3
mà -1<=sin x<=1
nên -1<=2m/3<=1
=>-3<=2m<=3
=>-3/2<=m<=3/2
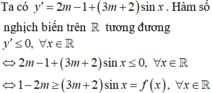
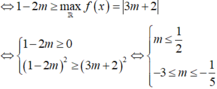


Pt có nghiệm: \(\Rightarrow m^2+\left(2m+1\right)^2\ge\left(3m+1\right)^2\)
\(\Rightarrow m^2+4m^2+4m+1\ge9m^2+6m+1\)
\(\Rightarrow-4m^2-2m\ge0\)
\(\Rightarrow-\dfrac{1}{2}\le m\le0\) thì pt có nghiệm.