Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giao điểm A của d1 và d2 là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-2y+5=0\\2x-3y+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow A\left(1;3\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-1\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-15=0\)

Đáp án: A
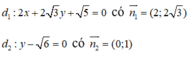
Gọi α là góc giữa hai đường thẳng d1, d2
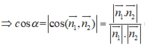
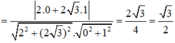
⇒ α = 30 °

Xét Δ và d1, hệ phương trình: 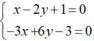 có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: 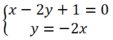 có nghiệm duy nhất (-1/5; 2/5) nên
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: 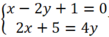 vô nghiệm
vô nghiệm
Vậy Δ // d3

Lời giải
Chọn C
Vectơ pháp tuyến của d1; d2 lần lượt là n 1 → ( 2 ; 1 ) ; n 2 → ( 1 ; 1 )
Cos( d1; d2) =


Ta có d 2 : 3 x − 2 y + 1 = 0 ⇔ 6 x − 4 y + 2 = 0
Ta có điểm A(-1; 1) thuộc đường thẳng d2,.
Vì hai đường thẳng d1 và d2 song song với nhau nên ta có:
d ( d 1 ; d 2 ) = d ( A ; d 1 ) = 6. ( − 1 ) − 4. ( − 1 ) + 5 6 2 + ( − 4 ) 2 = 3 52
ĐÁP ÁN D

- Xét d1 và d2 có : \(\left\{{}\begin{matrix}\overrightarrow{n_{d1}}\left(1;-3\right)\\\overrightarrow{n_{d2}}\left(1;-2\right)\end{matrix}\right.\)
\(\Rightarrow\cos\alpha=\left|\dfrac{\overrightarrow{n_{d1}}.\overrightarrow{n_{d2}}}{\left|\overrightarrow{n_{d1}}\right|.\left|\overrightarrow{n_{d2}}\right|}\right|=\left|\dfrac{1.1+\left(-2\right).\left(-3\right)}{\sqrt{\left(1^2+\left(-3\right)^2\right)\left(1^2+\left(-2\right)^2\right)}}\right|=\dfrac{7\sqrt{2}}{10}\)
\(\Rightarrow\alpha=~8^o\)
- Từ d1 và d2 ta có hệ phương trình \(\left\{{}\begin{matrix}x-3y=-1\\x-2y=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=17\\y=6\end{matrix}\right.\)
Vậy tọa độ giao điểm của d1 và d2 là ( 17; 6 ) .
Vectơ pháp tuyến của đường thẳng d1 là n1=(1;2)
Vectơ pháp tuyến của đường thẳng d2 là n2=(2;-4)
Gọi φ là góc giữa 2 đường thẳng ta có:
cos φ = n 1 . n 2 n 1 . n 2 = - 3 5
Chọn A.