Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
+ Để điểm đó dao động cực đại và cùng pha thì
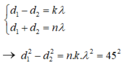
Mà
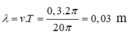
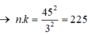
(nguyên)
Mặc khác
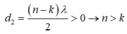
Bỏ qua k=0 vì không cắt ∆ .
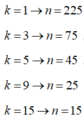
Vậy có 4 giá trị của k thỏa mãn điều kiện.
Với mỗi k thì cắt ∆ tại 2 điểm nên số cực đại cùng pha 2 nguồn là 8.

Đáp án D
Sóng tại M có biên độ triệt tiêu nên M là cực tiểu
![]()
Giữa M và đường trung trực AB có 5 đường cực đại nên M là cực tiểu có k = 5
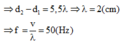

Đáp án A
Bước sóng: λ = v.T = v/f = 80/40 = 2cm
=> Khoảng cách ngắn nhất giữa hai điểm cực đại giao thoa trên đoạn thẳng S 1 S 2 là λ/2 = 1cm

Đáp án C
Bước sóng λ = v / f = 1 c m
Vì C dao động với biên độ cực đại và giữa điểm C và đường turng trực của AB còn có hai dãy cực đại khác nên C thuộc đường cực đại bậc 3
⇒ C A − C B = k λ = 3 c m
Mặt khác C A − C B = 2 A B − A B = 2 − 1 A B
⇒ 2 − 1 A B = 3 c m ⇒ A B = 3 2 − 1 c m
Vậy số điểm cực đại trên đường thẳng nối hai nguồn là:
2 A B λ + 1 = 2 3 2 − 1 + 1 = 15 đ i ể m

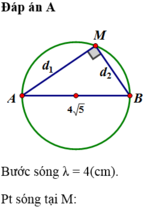
u M = 4 cos π d 2 - d 1 λ cos 30 πt - π d 2 + d 1 λ c m

d 2 - d 1 = 4 k d 2 + d 1 = 8 n d 1 2 + d 2 2 = 80 ⇔ d 1 = 4 n - 2 k d 2 = 4 n + 2 k 4 n - 2 k 2 + 4 n + 2 k 2 = 80 ⇔ k < 2 n ; n > 0 4 n 2 + k 2 = 10


Đáp án A
![]()
Xét trên đoạn AB :
Nếu ![]()
Nếu ![]()
![]()
![]()
→ có 6 giá trị của k
Số điểm trên (C) dao động với biên độ cực đại và cùng pha với hai nguồn là : 6 – 2 = 4 điểm






Đáp án A
Độ lệch pha của điểm M với hai nguồn là Δ φ = π λ d 2 + d 1
Điều kiện để M lệch pha π / 2 so với nguồn
Δ φ = π 2 d 2 + d 1 = π 2 + k π ⇔ d 2 + d 1 = 2 k + 1 2 λ 1
Vậy quỹ tích các điểm lệch pha π / 2 so với nguồn là đường elip thỏa mãn đều kiện (1) nhận S 1 và S 2 làm tiêu điểm
Điều kiện để các đường elip này nằm trong (E) là:
d 1 + d 2 ≤ d 1 N + d 2 N = 2 O N 2 + S 1 S 2 2 2 2
Mặt khác tổng các cạnh trong một tam giác lớn hơn cạnh còn lại nên S 1 S 2 < d 1 + d 2 3
Kết hợp (1), (2) và (3) ta có: S 1 S 2 < d 1 + d 2 ≤ 2 O N 2 + S 1 S 2 2 2
⇔ 27,6 < 2 k + 1 λ 2 ≤ 2 12 2 + 27,6 2 2 ⇔ 2,95 < k ≤ 4,07 ⇒ k = 3,4
Vậy có 2 đường elip nằm trong € mà các điểm trên đó lệch pha π / 2 so với nguồn.