Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\left(x-2\right)^3-x\left(x+1\right)\left(x-1\right)+6x\left(x-3\right)\)
\(=\left(x-2\right)^3-x\left(x^2-1\right)+6x^2-18x\)
\(=x^3-6x^2+12x-8-x^3+x+6x^2-18x\)
\(=-5x\)
Các câu còn lại lm tương tự nhé

Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !
\(\left(x+6\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}x+6=0\\2x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-6\\x=-\frac{1}{2}\end{cases}}\)
Vậy....
hk tốt
^^

b: \(\dfrac{4}{x+2}+\dfrac{2}{x-2}+\dfrac{5-6x}{4-x^2}\)
\(=\dfrac{4x-8+2x+4+6x-5}{\left(x-2\right)\left(x+2\right)}=\dfrac{12x-9}{\left(x-2\right)\left(x+2\right)}\)
c: \(\dfrac{x^3+2x}{x^3+1}+\dfrac{2x}{x^2-x+1}+\dfrac{1}{x+1}\)
\(=\dfrac{x^3+2x+2x^2+2x+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x^3+3x^2+3x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{\left(x+1\right)^3}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x^2+2x+1}{x^2-x+1}\)
e: \(\dfrac{7}{x}-\dfrac{x}{x+6}+\dfrac{36}{x^2+6x}\)
\(=\dfrac{7x+42-x^2+36}{x\left(x+6\right)}\)
\(=\dfrac{-x^2+7x+78}{x\left(x+6\right)}\)
\(=\dfrac{-x^2+13x-6x+78}{x\left(x+6\right)}\)
\(=\dfrac{-x\left(x-13\right)-6\left(x-13\right)}{x\left(x+6\right)}\)
\(=\dfrac{\left(13-x\right)\left(x+6\right)}{x\left(x+6\right)}=\dfrac{13-x}{x}\)

Bài 2:
a: \(\Leftrightarrow x^3-27-x\left(x^2-4\right)=1\)
\(\Leftrightarrow x^3-27-x^3+4x=1\)
=>4x-27=1
hay x=7
b: \(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6\left(x-1\right)^2+10=0\)
\(\Leftrightarrow6x^2+12-6x^2+12x-6=0\)
=>12x+6=0
hay x=-1/2

a: \(=\dfrac{2\left(x+2\right)\left(x-1\right)}{x+2}=2x-2\)
b: \(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}=x^2-3x+1\)
c: \(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}=x^2-2x+2\)
d: \(=\dfrac{x^2\left(x-3\right)}{x-3}=x^2\)

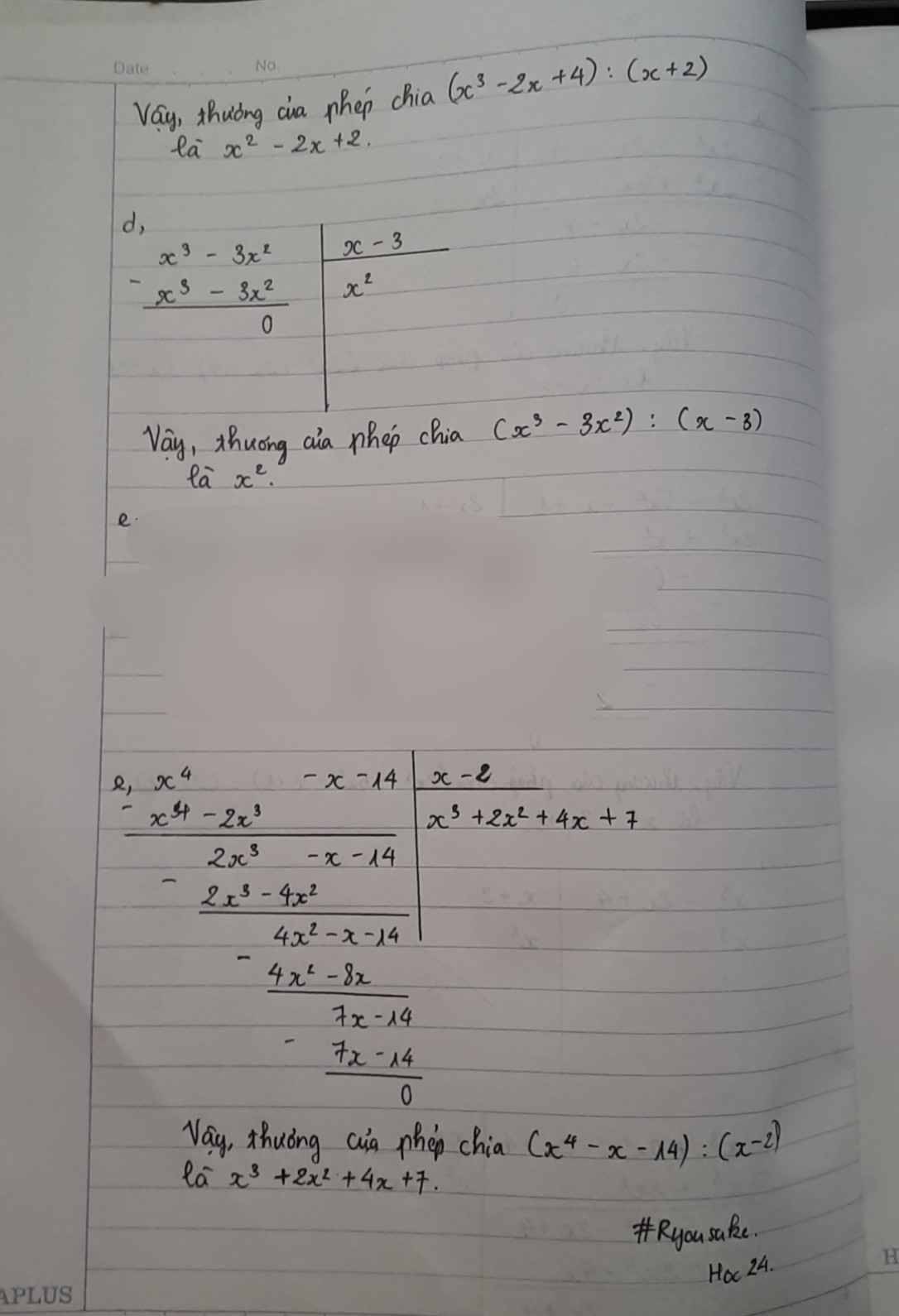

Câu 2:
a: \(\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=1\)
\(\Leftrightarrow x^3-27-x\left(x^2-4\right)=1\)
\(\Leftrightarrow x^3-27-x^3+4x=1\)
=>4x-27=1
=>4x=28
hay x=7
b: \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow x^3+3x^2+3x+1-\left(x^3-3x^2+3x-1\right)-6\left(x^2-2x+1\right)=-10\)
\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6=-10\)
\(\Leftrightarrow12x-4=-10\)
=>12x=-6
hay x=-1/2